题目内容
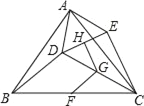
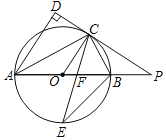
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若AF=6,EF=2![]() ,求⊙O的半径长.
,求⊙O的半径长.
【答案】(1)证明见解析(2)证明见解析(3)4
【解析】
(1)根据切线的性质得OC⊥AD,而AD⊥DP,则肯定判断OC∥AD,根据平行线的性质得∠DAC=∠OCA,加上∠OAC=∠OCA,所以∠OAC=∠DAC;
(2)根据圆周角定理由AB为⊙O的直径得∠ACB=90°,则∠BCE=45°,再利用圆周角定理得∠BOE=2∠BCE=90°,则∠OFE+∠OEF=90°,易得∠CFP+∠OEF=90°,再根据切线的性质得到∠OCF+∠PCF=90°,而∠OCF=∠OEF,根据等角的余角相等得到∠PCF=∠CFP,于是可判断△PCF是等腰三角形;
(3)连结OE.由AB为⊙O的直径,得到∠ACB=90°,根据角平分线的定义得到∠BCE=45°,设⊙O的半径为r,则OF=6-r,根据勾股定理列方程即可得到结论.
(1)证明:∵PD为⊙O的切线,
∴OC⊥DP,
∵AD⊥DP,
∴OC∥AD,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OAC=∠DAC,
∴AC平分∠DAB;
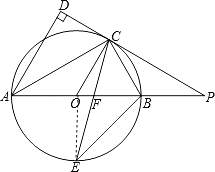
(2)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∵CE平分∠ACB,
∴∠BCE=45°,
∴∠BOE=2∠BCE=90°,
∴∠OFE+∠OEF=90°,
而∠OFE=∠CFP,
∴∠CFP+∠OEF=90°,
∵OC⊥PD,
∴∠OCP=90°,即∠OCF+∠PCF=90°,
而∠OCF=∠OEF,
∴∠PCF=∠CFP,
∴△PCF是等腰三角形;
(3)解:连结OE.
∵AB为⊙O的直径,∴∠ACB=90°,
∵CE平分∠ACB,∴∠BCE=45°,
∴∠BOE=90°,即OE⊥AB,
设⊙O的半径为r,则OF=6-r,
在Rt△EOF中,∵OE2+OF2=EF2,
∴r2+(6-r)2=(2![]() )2,
)2,
解得,r1=4,r2=2,
当r1=4时,OF=6-r=2(符合题意),
当r2=2时,OF=6-r=4(不合题意,舍去),
∴⊙O的半径r=4.

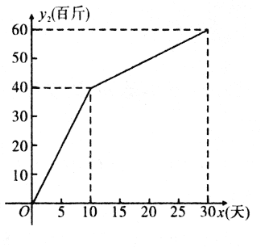
【题目】合肥周谷堆农副产品批发市场某商铺购进一批红薯,通过商店批发和在淘宝网上进行销售.首月进行了销售情况的统计,其中商店日批发量![]() (百斤)与时间
(百斤)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如下表所示;在淘宝网上的日销售量
为整数,单位:天)的部分对应值如下表所示;在淘宝网上的日销售量![]() (百斤)与时间
(百斤)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如图所示.
为整数,单位:天)的部分对应值如图所示.
时间 | 0 | 5 | 10 | 150 | 20 | 25 | 30 |
日批发量 | 025 | 40 | 45 | 40 | 25 | 0 |
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映![]() 与
与![]() 的变化规律,求出
的变化规律,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)设这个月中,日销售总量为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式,并求出当
之间的函数关系式,并求出当![]() 为何值时,日销售总量
为何值时,日销售总量![]() 最大,最大值为多少?
最大,最大值为多少?