题目内容
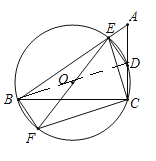
【题目】如图,在△ABC中,∠ACB=90°,过B,C两点的⊙O交AC于点D,交AB于点E,连接EO并延长交⊙O于点F.连接BF,CF.若∠EDC=135°,CF=![]() ,则AE2+BE2的值为 ( )
,则AE2+BE2的值为 ( )

A. 8 B. 12 C. 16 D. 20
【答案】C
【解析】
根据圆内接四边形的性质及邻补角的定义可得∠ADE=∠ABC=45°,再证得∠ADE=∠A=45°即可得AE=AD;根据直径所对的圆周角是直角可得∠FCE=90°,在Rt△EFC中求得EF=4;连接BD,可证得BD为为⊙O的直径,在Rt△BDE中根据勾股定理可得![]() ,由此即可得结论.
,由此即可得结论.
∵∠EDC=135°,
∴∠ADE=45°,∠ABC=180°-∠EDC =180°-135°=45°;
∵∠ACB=90°,
∴∠A=45°,
∴∠ADE=∠A=45°,
∴AE=AD,∠AED=90°;
∵EF 为⊙O的直径,
∴∠FCE=90°,
∵∠ABC=∠EFC=45°,CF=![]() ,
,
∴EF=4;
连接BD,
∵∠AED=90°,
∴∠BED=90°,
∴BD 为⊙O的直径,
∴BD=4;
在Rt△BDE中,![]() ,
,
∴AE2+BE2=16.
故选C.

练习册系列答案
相关题目



