Question

【题目】已知一张正方形ABCD纸片，边长AB＝2，按步骤进行折叠，如图1，先将正方形纸片ABCD对折，得到折痕EF；再折出矩形BCFE的对角线BF．

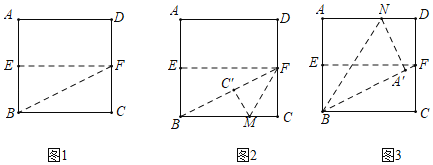
（1）如图2，将CF边折到BF上，得到折痕FM，点C的对应点为C'，求CM的长．

（2）如图3，将AB边折到BF上，得到折痕BN，点A的对应点为A'，求AN的长．

Answer 1

【答案】（1）CM＝；（2）AN＝﹣1．

【解析】

（1）根据正方形折叠求出边长，再根据勾股定理即可求出CM．

（2）方法同（1）直接勾股定理求解即可．

∵将正方形纸片ABCD对折，

∴CF＝DF＝1，

∴BF＝ ＝ ＝ ，

（1）∵将CF边折到BF上，

∴CF＝C'F＝1，∠C＝∠FC'M＝90°，CM＝C'M，

∴BC'＝﹣1，

∵tan∠FBC＝ ，

∴ ，

∴C'M＝，

∴CM＝ ；

（2）如图，连接NF，

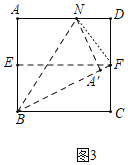
∵将AB边折到BF上，

∴AB＝A'B＝2，AN＝A'N，∠A＝∠NA'F＝90°，

∴A'F＝ ﹣2，

∵NF2＝DN2+DF2，NF2＝A'N2+A'F2，

∴（2﹣AN）2+1＝AN2+（﹣2）2，

∴AN＝﹣1．