题目内容
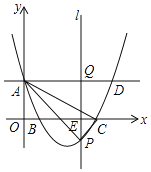
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与y轴的交点为A(0,3),与x轴的交点分别为B(2,0),C(6,0).直线AD∥x轴,在x轴上位于点B右侧有一动点E,过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P,Q.
(1)求抛物线的解析式;
(2)当点E在线段BC上时,求△APC面积的最大值;
(3)是否存在点P,使以A,P,Q为顶点的三角形与△AOB相似?若存在,求出此时点E的坐标;若不存在,请说明理由.
【答案】(1)y=![]() ﹣2x+3;(2)
﹣2x+3;(2)![]() ;(3)存在,(
;(3)存在,(![]() ,0)或(
,0)或(![]() ,0)或(14,0)
,0)或(14,0)
【解析】
(1)按交点式设成抛物线解析式,再将点A坐标代入,即可得出结论;
(2)先利用待定系数法求出直线AC解析式,进而表示出PF,利用三角形的面积公式得出S=﹣![]() (t﹣3)2+
(t﹣3)2+![]() ,即可得出结论;
,即可得出结论;
(3)①再分2<t<8和t>时,表示出AQ=t,PQ=﹣![]() t2+2t,再分两种情况,利用相似三角形的对应边成比例建立方程求解即可得出结论.
t2+2t,再分两种情况,利用相似三角形的对应边成比例建立方程求解即可得出结论.
(1)∵抛物线B(2,0)、C(6,0),
∴设抛物线为:![]() ,
,
把点A(0,3)代入![]() ,
,
得![]() ,
,
∴a![]() ,
,
∴该抛物线解析式为:![]() ;
;
(2)设直线AC的解析式为:![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴直线AC的解析式为:![]() ,
,
设△APC面积为S,
如图,设直线l与AC交点为F,

设P(t,![]() t2﹣2t+3)(2≤t≤6),则F(t,﹣
t2﹣2t+3)(2≤t≤6),则F(t,﹣![]() t+3),
t+3),
∴PF=﹣![]() t+3-(
t+3-(![]() t2﹣2t+3)
t2﹣2t+3)![]() t2+
t2+![]() t,
t,
∴S![]() t2
t2![]() ×6
×6
=﹣![]() 2+
2+![]() ,
,
∴当t=3时,S最大值![]() ,
,
即△APC面积的最大值为![]() ;
;
(3)存在点P,
理由:连接AB,则△AOB中,∠AOB=90°,
∵点A、B的坐标分别为(0,3)、(2,0),
∴AO=3,BO=2,
设点E的坐标为(t,0)(![]() >2),
>2),
则Q(t,3),P(t,![]() t2﹣2t+3),
t2﹣2t+3),
当![]() t2﹣2t+3=3时,此时,点P,Q重合,即t=0(舍)或t=8,不能构成△APQ,
t2﹣2t+3=3时,此时,点P,Q重合,即t=0(舍)或t=8,不能构成△APQ,
∴t≠8,
①当2<t<8时,AQ=t,PQ=3-(![]() t2﹣2t+3)=﹣
t2﹣2t+3)=﹣![]() t2+2t,
t2+2t,
当△AOB∽△AQP时,
∴![]() ,
,
∴ ,
,
解得:t=0(舍)或t=![]() ,
,
∴点E的坐标为(![]() ,0),
,0),
若△AOB∽△PQA,
则![]() ,
,
∴ ,
,
解得:t=0(舍)或t=2(舍),
②当t>8时,AQ=t, PQ=![]() t2﹣2t+3-3=
t2﹣2t+3-3=![]() t2-2t,
t2-2t,
若△AOB∽△AQP,
则∴![]() ,
,
∴ ,
,
解得:t=0(舍)或t=![]() ,
,
∴点E的坐标为(![]() ,0),
,0),
若△AOB∽△PQA,
则![]() ,
,
即 ,
,
解得:t=0(舍)或t=14,
∴点E的坐标为(14,0),
综上所述,点E的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(14,0).
,0)或(14,0).

 优学名师名题系列答案
优学名师名题系列答案