��Ŀ����
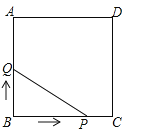
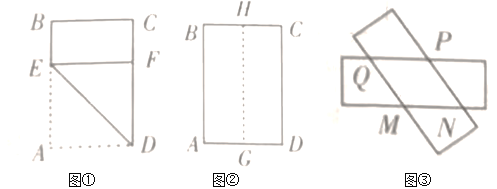
����Ŀ����ͼ1�����ı���ABCD��GFED���������Σ���Ȼͼ����AG��CE��AG��CE��
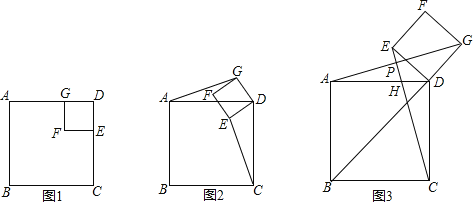
��1����������GFED��D��ת����ͼ2��λ��ʱ��AG��CE�Ƿ�������������������֤����������������˵�����ɣ�
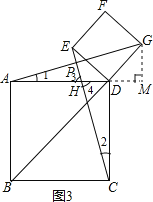
��2����������GFED��D��ת��B��D��G��һ��ֱ�ߣ���ͼ3����ʱ������CE����CE�ֱ�AG��AD��P��H��
����֤��AG��CE��
�������AD��2![]() ��DG��
��DG��![]() ����CE�ij���
����CE�ij���
���𰸡���1��AG��CE��������2���������������5![]()
��������
��1�����������������Լ�ȫ�������ε��ж��ĺܴ���AGD�ա�CED��SAS�����ɵó��𰸣�
��2���ٸ��ݣ�1���ó���1����2�������á�3����4����4+��2��90�����ɵó���3+��1��90���������ó��𰸣�
�����õ���ֱ�������ε����ʿɵó�MD��MG��![]() ���������ù��ɶ������CE�ij���
���������ù��ɶ������CE�ij���
��1���⣺AG��CE������
���ɣ����ı���ABCD���ı���DEFG�������Σ�
��GD��DE��AD��DC��
��GDE����ADC��90����
���GDA��90������ADE����EDC��
����AGD����CED��
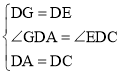
���AGD�ա�CED��SAS����
��AG��CE��
��2��֤�������ɣ�1����֪��AGD�ա�CED��
���1����2��
�ߡ�3����4����4+��2��90����
���3+��1��90����
���APH��90����
��AG��CH��
�ڽ⣺��G��GM��AD��M��
��BD��������ABCD�ĶԽ��ߣ�
���ADB����GDM��45����
���DGM��45����
��DG��![]() ��
��
��MD��MG��![]() ��
��
��Rt��AMG�У��ɹ��ɶ�������
��CE��AG��5![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij�о���Ľ�ͨ���ѿɷ�Ϊ��ͨ���ߡ���ͨ����ʹ��ȼ�ϡ���ͨ����ά�ޡ����ڹ�����ͨ�����м佻ͨ����.����ͳ�ƾָ��ݵ�������Ȩ�ؼ�����۸���Ƿ������㵱�����ͨ���Ѽ۸��ƽ���Ƿ�.2017����е��й��������±���ʾ.
��ͨ���� | ��ͨ����ʹ��ȼ�� | ��ͨ����ά�� | ���ڹ�����ͨ | ���м佻ͨ | |
ռ��ͨ���ѵı��� | 22% | 13% | 5% | P | 26% |
�����һ��۸���Ƿ� | 1.5% | m% | 2% | 0.5% | 1% |
��1����p��ֵ��
��2����2017����еľ���ͨ���������һ��۸��ƽ���Ƿ�Ϊ1.25%����m��ֵ.