题目内容
【题目】“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
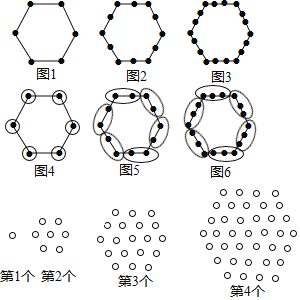
例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;所以容易求出图10、图n中黑点的个数分别是 、 .
请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题:
(1)第5个点阵中有 个圆圈;第n个点阵中有 个圆圈.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
【答案】60个,6n个;(1)61;3n2﹣3n+1,(2)小圆圈的个数会等于271,它是第10个点阵.
【解析】根据规律求得图10中黑点个数是6×10=60个;图n中黑点个数是6n个;
(1)第2个图中2为一块,分为3块,余1,
第2个图中3为一块,分为6块,余1;
按此规律得:第5个点阵中5为一块,分为12块,余1,得第n个点阵中有:n×3(n﹣1)+1=3n2﹣3n+1,
(2)代入271,列方程,方程有解则存在这样的点阵.
图10中黑点个数是6×10=60个;图n中黑点个数是6n个,
故答案为:60个,6n个;
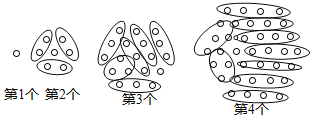
(1)如图所示:第1个点阵中有:1个,
第2个点阵中有:2×3+1=7个,
第3个点阵中有:3×6+1=17个,
第4个点阵中有:4×9+1=37个,
第5个点阵中有:5×12+1=60个,
…
第n个点阵中有:n×3(n﹣1)+1=3n2﹣3n+1,
故答案为:60,3n2﹣3n+1;
(2)3n2﹣3n+1=271,
n2﹣n﹣90=0,
(n﹣10)(n+9)=0,
n1=10,n2=﹣9(舍),
∴小圆圈的个数会等于271,它是第10个点阵.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案