题目内容
如果一个直角三角形斜边上的中线与斜边所成的锐角为50°,那么这个直角三角形的较小内角的度数为______.
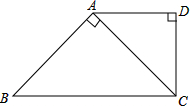
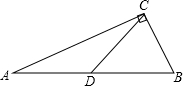
如图,∵CD是Rt△ABC斜边上的中线,
∴CD=AD=DB,
∴∠A=∠ACD,
∵斜边上的中线与斜边所成的锐角为50°,即∠BDC=50°,
∴∠BDC=∠A+∠ACD=2∠A=50°,
解得∠A=25°,
另一个锐角∠B=90°-25°=65°,
∴这个直角三角形的较小内角的度数为25°.
故答案为:25°.
∴CD=AD=DB,
∴∠A=∠ACD,
∵斜边上的中线与斜边所成的锐角为50°,即∠BDC=50°,
∴∠BDC=∠A+∠ACD=2∠A=50°,
解得∠A=25°,
另一个锐角∠B=90°-25°=65°,
∴这个直角三角形的较小内角的度数为25°.
故答案为:25°.


练习册系列答案
相关题目