题目内容
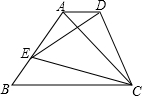
如图，在△ABC中，AD交边BC于点D，∠BAD=15°，∠ADC=4∠BAD，DC=2BD．
（1）求∠B的度数；
（2）求证：∠CAD=∠B．
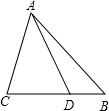
（1）求∠B的度数；
（2）求证：∠CAD=∠B．
（1）∵∠BAD=15°，∠ADC=4∠BAD，
∴∠ADC=60°，
∴∠B=60°-15°=45°；
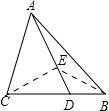（2）证明：过C作CE⊥AD于E，连接EB．
∵∠ECD=90°-60°=30°
∴DC=2ED，
∵DC=2BD，
∴ED=BD，
∴∠DBE=∠DEB=∠ECD=30°，
∴∠EBA=45°-30°=15°=∠BAD，
∴AE=EC=EB，
∴∠CAD=∠ABD=45°．
∴∠ADC=60°，
∴∠B=60°-15°=45°；
（2）证明：过C作CE⊥AD于E，连接EB．∵∠ECD=90°-60°=30°
∴DC=2ED，
∵DC=2BD，
∴ED=BD，
∴∠DBE=∠DEB=∠ECD=30°，
∴∠EBA=45°-30°=15°=∠BAD，
∴AE=EC=EB，
∴∠CAD=∠ABD=45°．
练习册系列答案
名校课堂系列答案
相关题目
