题目内容
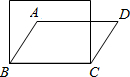
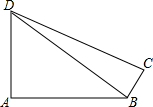
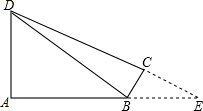
如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5
cm,求DB、DC的长.(直角三角形中,30°角所对边等于斜边的一半)
| 3 |

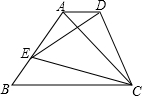
如图,延长AB、DC相交于点E,
∵∠ADC=60°,BC=2cm,AD=5
cm,
∴BE=2BC=2×2=4(cm),
DE=2AD=2×5
=10
(cm),
在Rt△BCE中,CE=
=
=2
(cm),
∴DC=DE-CE=10
-2
=8
(cm),
在Rt△BCD中,DB=
=
=14(cm).
∵∠ADC=60°,BC=2cm,AD=5
| 3 |
∴BE=2BC=2×2=4(cm),
DE=2AD=2×5
| 3 |
| 3 |
在Rt△BCE中,CE=
| BE2-BC2 |
| 42-22 |
| 3 |
∴DC=DE-CE=10
| 3 |
| 3 |
| 3 |
在Rt△BCD中,DB=
| DC2+BC2 |
(8
|


练习册系列答案
相关题目