题目内容
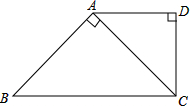
已知：如图，在△ABC中，CD⊥AB，垂足为D，∠A=30°，∠B=45°，AC=4．
求CD和AB的长．
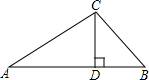
求CD和AB的长．
∵CD⊥AB，
∴∠ADC=∠BDC=90°，
∵∠A=30°，AC=4．
∴CD=
AC=2，
由勾股定理得：AD=
=2
，
∵∠BDC=90°，∠B=45°，
∴∠BCD=45°=∠B，
∴BD=DC=2，
∴AB=2
+2．
∴∠ADC=∠BDC=90°，
∵∠A=30°，AC=4．
∴CD=
| 1 |
| 2 |
由勾股定理得：AD=
| 42-22 |
| 3 |
∵∠BDC=90°，∠B=45°，
∴∠BCD=45°=∠B，
∴BD=DC=2，
∴AB=2
| 3 |
练习册系列答案
学业测评一课一测系列答案
相关题目
