题目内容
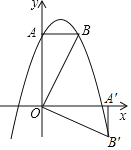
【题目】如图,已知抛物线y=ax2+bx+4经过点(2,4),(-2,-2),交y轴于点A,过点A作AB⊥y轴交抛物线于点B.
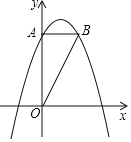
(1)求抛物线的解析式.
(2)将△OAB绕点O顺时针旋转90°得到△OA'B',试判断B'是否落在抛物线上,并说明理由.
【答案】(1)y=-![]() ;(2)B'落在抛物线上,理由见解析;
;(2)B'落在抛物线上,理由见解析;
【解析】
(1)直接利用已知点代入函数解析式进而得出答案;
(2)利用已知得出A,B点坐标,再利用旋转的性质得出B′点坐标,进而判断得出答案.
(1)将点(2,4),(-2,-2),代入函数解析式得:
![]() ,
,
解得:
 ,
,
故抛物线解析式为:y=-![]() ;
;
(2)B'落在抛物线上,
理由:∵抛物线与y轴于点A,
∴x=0时,y=4,即A(0,4),
当y=4时,4=-![]() ,
,
解得:x1=0,x2=2,
∴B(2,4),
∵将△OAB绕点O顺时针旋转90°得到△OA'B',
∴B′(4,-2),
当x=4时,-![]() ×4+4=-2,
×4+4=-2,
故B'落在抛物线上.

练习册系列答案
相关题目