题目内容
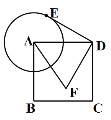
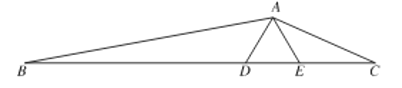
【题目】如图,正方形![]() 中,
中,![]() 经顺时针旋转后与
经顺时针旋转后与![]() 重合.
重合.

(1)旋转中心是点 ,旋转了 度;
(2)如果![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)A,90;(2)![]() .
.
【解析】
(1)根据正方形的性质得AB=AD,∠BAD=90°,则根据旋转的定义得到△ADE绕点A顺时针旋转90°后与△ABF重合;
(2)根据旋转的性质得BF=DE,S△ABF=S△ADE,利用CF=CB+BF=8得到BC+DE=8,再加上CE=CD-DE=BC-DE=4,于是可计算出BC=6,于是得到结论.
解:(1)∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴△ADE绕点A顺时针旋转90°后与△ABF重合,
即旋转中心是点A,旋转了90度;
故答案为A,90;
(2)∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴BF=DE,S△ABF=S△ADE,
而CF=CB+BF=8,
∴BC+DE=8,
∵CE=CD-DE=BC-DE=4,
∴BC=6,
∴AC=![]() BC=6
BC=6![]() .
.
故答案为:(1)A,90;(2)![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目