题目内容
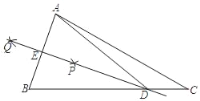
【题目】如图,在锐角△ABC中,小明进行了如下的尺规作图:
①分别以点A、B为圆心,以大于![]() AB的长为半径作弧,两弧分别相交于点P、Q;
AB的长为半径作弧,两弧分别相交于点P、Q;
②作直线PQ分别交边AB、BC于点E、D.
(1)小明所求作的直线DE是线段AB的 ;
(2)联结AD,AD=7,sin∠DAC=![]() ,BC=9,求AC的长.
,BC=9,求AC的长.
【答案】(1)线段AB的垂直平分线(或中垂线);(2)AC=5![]() .
.
【解析】
(1)垂直平分线:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线
(2)根据题意垂直平分线定理可得AD=BD,得到CD=2,又因为已知sin∠DAC=![]() ,故可过点D作AC垂线,求得DF=1,利用勾股定理可求得AF,CF,即可求出AC长.
,故可过点D作AC垂线,求得DF=1,利用勾股定理可求得AF,CF,即可求出AC长.
(1)小明所求作的直线DE是线段AB的垂直平分线(或中垂线);
故答案为线段AB的垂直平分线(或中垂线);
(2)过点D作DF⊥AC,垂足为点F,如图,
∵DE是线段AB的垂直平分线,
∴AD=BD=7
∴CD=BC﹣BD=2,
在Rt△ADF中,∵sin∠DAC=![]() ,
,
∴DF=1,
在Rt△ADF中,AF=![]() ,
,
在Rt△CDF中,CF=![]() ,
,
∴AC=AF+CF=![]() .
.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目