Question

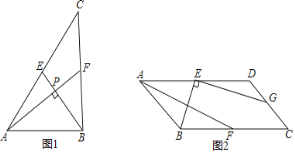
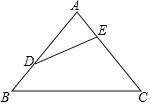
【题目】如图，△ABC中，AB＝AC，∠A＝80°，点D，E分别在边AB，AC上，且DA＝DE＝CE．

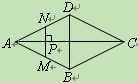
（1）求作点F，使得四边形BDEF为平行四边形；（要求：尺规作图，保留痕迹，不写作法）

（2）连接CF，写出图中经过旋转可完全重合的两个三角形，并指出旋转中心和旋转角．

Answer 1

【答案】(1)见解析;(2)见解析;

【解析】

(1)根据作一个角等于已知角的方法，作∠ABF=∠ADE，然后再截取出BF=DE，连接EF，则四边形BDEF即为所求；

(2)由已知以及所作图形可推导得出AE＝FE，再由EF∥AB，可得∠FEC＝∠A＝80°，继而根据∠DEA＝∠A＝80°，可得∠AEF＝∠DEC＝100°，由此即可得出△EAD绕点E逆时针旋转100°可得到△EFC．

(1)如图，四边形BDEF为所作；

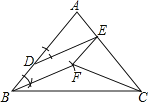
(2)∵四边形BDEF为平行四边形，

∴EF＝BD，EF∥BD，

∵AB＝AC，AD＝CE，

∴BD＝AE，

∴AE＝FE，

∵EF∥AB，

∴∠FEC＝∠A＝80°，

而∠DEA＝∠A＝80°，

∴∠AEF＝∠DEC＝100°，

∴△EAD绕点E逆时针旋转100°可得到△EFC．