题目内容
【题目】如图，在△ABC中，AD⊥BC，垂足为D，AD＝4，BD＝2，CD＝8．
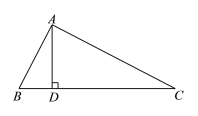
（1）求证：∠BAC＝90°；
（2）P为BC边上一点，连接AP，若△ABP为等腰三角形，请求出BP的长．
【答案】（1）详见解析；（2）BP的长为4或5或2
．
【解析】
（1）先利用勾股定理求出
的长度，然后
满足勾股定理AB2＋AC2＝BC2，则说明∠BAC＝90°；
（2）若△ABP为等腰三角形，分三种情况，
分别对这三种情况进行讨论即可.
（1）证明：∵AD⊥BC，AD＝4，BD＝2，CD＝8.
∴AB2＝ AD2＋BD2＝20， AC2＝AD2＋CD2＝80．
∵BC2＝(BD＋CD)2＝100， ∴AB2＋AC2＝BC2．
∴∠BAC＝90°．
（2）①
，
②
,
③
,P是BC中点，
综上所述，BP的长为4或5或2
练习册系列答案
相关题目
【题目】今年5月，某大型商业集团随机抽取所属的m家商业连锁店进行评估，将各连锁店按照评估成绩分成了A、B、C、D四个等级，绘制了如图尚不完整的统计图表．
评估成绩n（分） | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n＜90 | B | |
70≤n＜80 | C | 15 |
n＜70 | D | 6 |
根据以上信息解答下列问题：
（1）求m的值；
（2）在扇形统计图中，求B等级所在扇形的圆心角的大小；（结果用度、分、秒表示）
（3）从评估成绩不少于80分的连锁店中任选2家介绍营销经验，求其中至少有一家是A等级的概率．
