题目内容
【题目】已知甲、乙两地相距3200 m，小王、小李分别从甲、乙两地同时出发，相向而行，相遇后两人立即返回到各自出发地并停止行进．已知小李的速度始终是60 m/min，小王在相遇后以匀速返回，但比小李晚回到原地。在整个行进过程中，他们之间的距离y（m）与行进的时间t（min）之间的函数关系如图中的折线段AB—BC—CD所示，请结合图像信息解答下列问题：
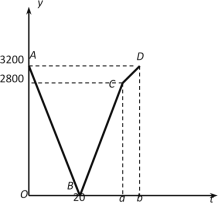
（1）小王返回时的速度= m/min，a＝ ，b＝ ；
（2）当t为何值时，小王、小李两人相距800 m？
【答案】（1）80, 40，45；（2）两人出发15min或
min时，相距800米．
【解析】
（1）根据小李相遇前后的速度不变，可先求出a的值，再利用BC段，求出小王的速度，然后利用CD段先求出小王到达目的地所需的时间，则b可求.
（2）分别用待定系数法求出直线AB,BC的函数解析式，令y＝500则可求出t的值.
∵小李相遇前后的速度不变
∴小李相遇前后所用的时间相同，都是20min
在BC段，小王、小李20min相距2800米，则小王的速度为
在CD段，
小王到达目的地还需要
，
（2）解：设AB对应的函数表达式为y＝k1t＋b1（0＜t≤20）．
由A(0，3200)，B(20，0)可求得：y＝－160t＋3200．
设BC对应的函数表达式为y2＝k2t＋b2（20＜t≤40）．
由C(20，0)，D(40，2800)可求得：y＝140t－2800．
当y＝500时，由－160t＋3200＝800可得t＝15；
由140t－2800＝800可得t＝．
综上，两人出发15min或min时，相距800米．
【题目】某班“数学兴趣小组”对函数y=|x|-2的图象特征进行了探究，探究过程如下：
⑴自变量x的取值范围是全体实数，x与y的几组对应值如下：
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 1 | m | -1 | -2 | n | 0 | 1 | 2 | … |
其中，m= ，n= .
⑵根据表中数据，在如图所示的平面直角坐标系中描点，并画出函数图象；
⑶观察函数图象，写出一条特征： .
【题目】某校团委组织“阳光助残”献爱心捐款活动，九年级（2）班学生捐款如表：
捐款金额（元） | 5 | 10 | 15 | 20 |
人数（人） | 13 | 16 | 17 | 10 |
学生捐款的中位数和众数是（ ）
A. 10元，15元 B. 15元，15元 C. 10元，20元 D. 16元，17元
