题目内容
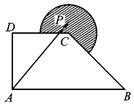
【题目】如图,AB为⊙O的直径,AB=4 ![]() ,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( )
,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( ) 
A.随点C的运动而变化,最大值为4
B.随点C的运动而变化,最大值为4 ![]()
C.随点C的运动而变化,最小值为2
D.随点C的运动而变化,但无最值
【答案】B
【解析】解:如图,连接OC, ∵△BCD是等边三角形,
∴∠BDC=60°,CD=BD,
在△OCD和△OBD中, 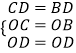 ,
,
∴△OCD≌△OBD(SSS),
∴∠BDO=∠CDO= ![]() ∠BDC=30°,
∠BDC=30°,
过点O作OF⊥BD于F,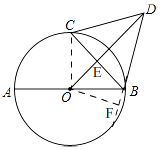
在Rt△ODF中,∠BDO=30°,
∴OD=2OF,
当点C在运动的过程中,OD要最大,即OF最大,而OF最大=OB,
∴OD最大=2OF最大=2OB=AB=4 ![]() .
.
故选B.
方法二、如图2,连接OC,
将△OCD绕点C顺时针旋转60°,则点D落在点B处,OD和⊙O相交于H,
连接OH,CH,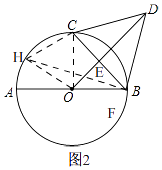
同方法一,得出∠ODC=30°,
∴∠CBH=30°,
∴∠COH=60°,
∴△COH是等边三角形,
∴HC=OC,∠OCH=60°,
∵△BCD是等边三角形,
∴CD=BC,∠BCD=60°,
∴∠OCD=∠HCB,
在△OCD和△HCB中, 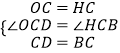 ,
,
∴△OCD≌△HCB(SAS),
∴OD=BH,
∵BH是⊙O的弦,
∴BH最大=AB=4 ![]() ,
,
即:OD最大=4 ![]() ,
,
故选B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目