题目内容
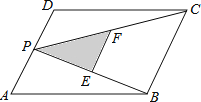
【题目】如图所示,抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于C点,且A(﹣2,0)、B(4,0),其顶点为D,连接BD,点P是线段BD上的一个动点(不与B、D重合),过点P作y轴的垂线,垂足为E,连接BE.
(1)求抛物线的解析式,并写出顶点D的坐标;
(2)设P点的坐标为(x,y),△PBE的面积为S,求S与x之间的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取值最大值时,过点P作x轴的垂线,垂足为F,连接EF,△PEF沿直线EF折叠,点P的对应点为点P′,请直接写出P′点的坐标,并判断点P′是否在该抛物线上.
【答案】
(1)
解:∵抛物线y=ax2+bx+4(a≠0)经过A(﹣2,0)、B(4,0)两点
∴把(﹣2,0)、B(4,0)代入抛物线得:a=﹣![]() ,b=1,
,b=1,
∴抛物线解析式为:y=﹣![]() x2+x+4.
x2+x+4.
∴顶点D的坐标为(1,![]() );
);
(2)
解:设直线BD解析式为:y=kx+b(k≠0),把B、D两点坐标代入,
得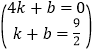 ,
,
解得k=﹣![]() ,b=6,
,b=6,
直线BD解析式为y=﹣![]() x+6,
x+6,
S=![]() PEOE,
PEOE,
S=![]() PEOE=
PEOE=![]() xy=
xy=![]() x(﹣
x(﹣![]() x+6)=﹣
x+6)=﹣![]() x2+3x,
x2+3x,
∵顶点D的坐标为(1,![]() ),B(4,0)
),B(4,0)
∴1<x<4,
∴S=﹣![]() x2+3x(1<x<4),
x2+3x(1<x<4),
S=﹣![]() (x2﹣4x++4)+3,
(x2﹣4x++4)+3,
=﹣![]() (x﹣2)2+3,
(x﹣2)2+3,
∴当x=2时,S取得最大值,最大值为3.
(3)
解:当S取得最大值,x=2,y=3,
∴P(2,3),
∴四边形PEOF是矩形.
作点P关于直线EF的对称点P′,连接P′E,P′F.
过P′作P′H⊥y轴于H,P′F交y轴于点M,
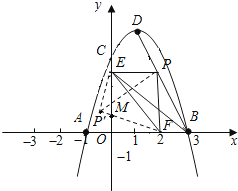
设MC=m,则MF=m,P′M=3﹣m,P′E=2,
在Rt△P′MC中,由勾股定理,
22+(3﹣m)2=m2,
解得m=![]() ,
,
∵CMP′H=P′MP′E,
∴P′H=![]() ,
,
由△EHP′∽△EP′M,
可得![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:EH=![]() .
.
∴OH=3﹣![]() =
=![]() .
.
∴P′坐标(﹣![]() ,
,![]() ).不在抛物线上.
).不在抛物线上.
【解析】(1)本题需先根据抛物线y=ax2+bx+4(a≠0)经过A(﹣2,0)、B(4,0)两点,分别求出a、b的值,再代入抛物线y=ax2+bx+4即可求出它的解析式.
(2)本题首先设出BD解析式y=kx+b,再把B、D两点坐标代入求出k、b的值,得出BD解析式,再根据面积公式即可求出最大值.
(3)本题需先根据(2)得出最大值来,求出点P的坐标,得出四边形PEOF是矩形,再作点P关于直线EF的对称点P′设出MC=m,则MF=m.从而得出P′M与P′E的值,根据勾股定理,得出m的值,再由△EHP′∽△EP′M,得出EH和OH的值,最后求出P′的坐标,判断出不在抛物线上.

【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 6 |
第3组 | 35≤x<40 | 14 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?