题目内容
【题目】如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为 ![]() ,且点P在图中阴影部分(包括边界)运动.若
,且点P在图中阴影部分(包括边界)运动.若 ![]() ,其中x,y∈R,则4x﹣y的最大值为( )
,其中x,y∈R,则4x﹣y的最大值为( ) 
A.![]()
B.![]()
C.2
D.![]()
【答案】B
【解析】解:以A为坐标原点,AB为x轴,AD为y轴建立平面直角坐标系,则 A(0,0),D(0,1),C(1,1),B(2,0),
直线BD的方程为x+2y﹣2=0,C到BD的距离d= ![]()
∴圆弧以点C为圆心的圆方程为(x﹣1)2+(y﹣1)2= ![]() ,
,
设P(m,n)则 ![]() =(m,n),
=(m,n),![]() =(0,1),
=(0,1), ![]() =(2,0),
=(2,0), ![]() =(﹣1,1)
=(﹣1,1)
若 ![]() ,
,
∴(m,n)=(2x﹣y,y)
∴m=2x﹣y,n=y
∵P在圆内或圆上
∴(2x﹣y﹣1)2+(y﹣1)2≤ ![]() ,
,
设4x﹣y=t,则y=4x﹣t,代入上式整理得80x2﹣(48t+32)x+8t2+7≤0,
设f(x)=80x2﹣(48t+32)x+8t2+7≤0,x∈[ ![]() ,
, ![]() ],
],
则  ,
,
解得2≤t≤3+ ![]() ,
,
故4x﹣y的最大值为3+ ![]() ,
,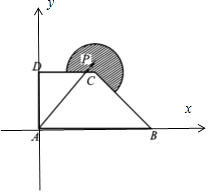
故选:B

练习册系列答案
相关题目
【题目】某地区住宅用电之电费计算规则如下:每月每户不超过50度时,每度以4元收费;超过50度的部分,每度以5元收费,并规定用电按整数度计算(小数部份无条件舍去) .
(1)下表给出了今年3月份A,B两用户的部分用电数据,请将表格数据补充完整,
电量(度) | 电费(元) | |
A | 240 | |
B | ||
合计 | 90 |
(2)若假定某月份C用户比D用户多缴电费38元,求C用户该月可能缴的电费为多少?