题目内容
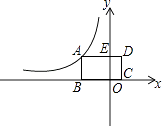
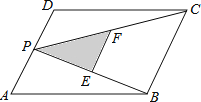
【题目】如图,在正方形ABCD中,点E、F分别在BC、CD上,且BE=DF,若∠EAF=30°,则sin∠EDF= . 
【答案】![]()
【解析】解:∵四边形ABCD是正方形, ∴AB=AD,∠B=∠ADF=∠BAD=90°,
在△ABE和△ADF中,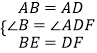 ,
,
∴△ABE≌△ADF,
∴∠BAE=∠FAD,
∵∠EAF=30°,
∴∠BAE=∠FAD=30°,
设正方形ABCD边长为a,
则tan30°= ![]() ,
,
∴BE= ![]() a,
a,
∴EC=a﹣ ![]() a,DE=
a,DE= ![]() =
= ![]() a
a
∴sin∠EDF= ![]() =
= ![]() =
= ![]()
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目
【题目】某地区住宅用电之电费计算规则如下:每月每户不超过50度时,每度以4元收费;超过50度的部分,每度以5元收费,并规定用电按整数度计算(小数部份无条件舍去) .
(1)下表给出了今年3月份A,B两用户的部分用电数据,请将表格数据补充完整,
电量(度) | 电费(元) | |
A | 240 | |
B | ||
合计 | 90 |
(2)若假定某月份C用户比D用户多缴电费38元,求C用户该月可能缴的电费为多少?