ƒøƒ⁄»ð
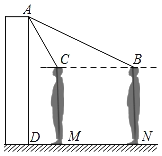
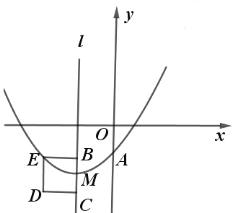
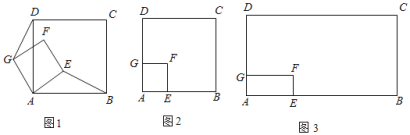
°æƒø°ø£®1£©Œ ÂÃΩæø£∫»ÁÕº1À˘ 棨”–π´π≤∂•µ„Aµƒ¡Ω∏ˆ’˝∑Ω–ŒABCD∫Õ’˝∑Ω–ŒAEFG£ÆAE£ºAB£¨¡¨Ω”BE”ÎDG£¨«Î≈–∂œœþ∂ŒBE”Îœþ∂ŒDG÷ƺ‰”–‘ı—˘µƒ ˝¡øπÿœµ∫ÕŒª÷√πÿœµ£Æ≤¢«ÎÀµ√˜¿Ì”…£Æ
£®2£©¿ÌΩ‚”¶”√£∫»ÁÕº2À˘ 棨”–π´π≤∂•µ„Aµƒ¡Ω∏ˆ’˝∑Ω–ŒABCD∫Õ’˝∑Ω–ŒAEFG£¨AE£ºAB£¨AB£Ω10£¨Ω´’˝∑Ω–ŒAEFG»∆µ„A‘⁄∆Ω√ʃ⁄»Œ“‚–˝◊™£¨µ±°œABE£Ω15°„£¨«“µ„D°¢E°¢G»˝µ„‘⁄Õ¨“ªÃı÷±œþ…œ ±£¨«Î÷±Ω”–¥≥ˆAEµƒ≥§°° °°£ª
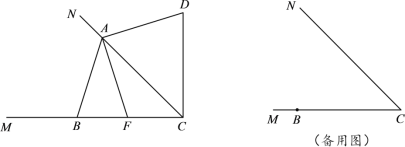
£®3£©Õÿ’𔶔√£∫»ÁÕº3À˘ 棨”–π´π≤∂•µ„Aµƒ¡Ω∏ˆæÿ–ŒABCD∫Õæÿ–ŒAEFG£¨AD£Ω4![]() £¨AB£Ω4
£¨AB£Ω4![]() £¨AG£Ω4£¨AE£Ω4
£¨AG£Ω4£¨AE£Ω4![]() £¨Ω´æÿ–ŒAEFG»∆µ„A‘⁄∆Ω√ʃ⁄»Œ“‚–˝◊™£¨¡¨Ω”BD£¨DE£¨µ„M£¨N∑÷± «BD£¨DEµƒ÷–µ„£¨¡¨Ω”MN£¨µ±µ„D°¢E°¢G»˝µ„‘⁄Õ¨“ªÃı÷±œþ…œ ±£¨«Î÷±Ω”–¥≥ˆMNµƒ≥§°° °°
£¨Ω´æÿ–ŒAEFG»∆µ„A‘⁄∆Ω√ʃ⁄»Œ“‚–˝◊™£¨¡¨Ω”BD£¨DE£¨µ„M£¨N∑÷± «BD£¨DEµƒ÷–µ„£¨¡¨Ω”MN£¨µ±µ„D°¢E°¢G»˝µ„‘⁄Õ¨“ªÃı÷±œþ…œ ±£¨«Î÷±Ω”–¥≥ˆMNµƒ≥§°° °°
°æ¥∞∏°ø£®1£©BE£ΩDG£¨BE°ÕDG£¨º˚Ω‚Œˆ£ª£®2£©5![]() ©Å5£ª£®3£©6
©Å5£ª£®3£©6![]() ªÚ8
ªÚ8![]()
°æΩ‚Œˆ°ø
£®1£©”…°∞SAS°±ø…÷§°˜GAD°’°˜EAB£¨ø…µ√BE£ΩDG£¨°œADG£Ω°œABE£¨”…÷±Ω«»˝Ω«–Œµƒ–‘÷ ø…µ√BE°ÕDG£ª
£®2£©”…°∞SAS°±ø…÷§°˜GAD°’°˜EAB£¨ø…µ√BE£ΩDG£¨°œADG£Ω°œABE£Ω15°„£¨ø…µ√°œDEB£Ω90°„£¨”…÷±Ω«»˝Ω«–Œµƒ–‘÷ ø…«ÛΩ‚£ª
£®3£©∑÷¡Ω÷÷«ÈøˆÃ÷¬€£¨Õ®π˝÷§√˜°˜AGD°◊°˜AEB£¨ø…µ√![]() £¨°œDGA£Ω°œAEB£¨”…π¥π…∂®¿Ì∫Õ»˝Ω«–Œ÷–Œªœþ∂®¿Ìø…«ÛΩ‚£Æ
£¨°œDGA£Ω°œAEB£¨”…π¥π…∂®¿Ì∫Õ»˝Ω«–Œ÷–Œªœþ∂®¿Ìø…«ÛΩ‚£Æ
Ω‚£∫£®1£©BE£ΩDG£¨BE°ÕDG£¨
¿Ì”…»Áœ¬£∫»ÁÕº1£∫—”≥§BEΩªAD”⁄N£¨ΩªDG”⁄H£¨

°þÀƒ±þ–ŒABCD «’˝∑Ω–Œ£¨Àƒ±þ–ŒAEFG «’˝∑Ω–Œ£¨
°ýAG£ΩAE£¨AB£ΩAD£¨°œGAE£Ω°œDAB£Ω90°„£¨
°ý°œGAD£Ω°œEAB£¨
°ý°˜GAD°’°˜EAB£®SAS£©£¨
°ýBE£ΩDG£¨°œADG£Ω°œABE£¨
°þ°œABE+°œANB£Ω90°„£¨
°ý°œADG+°œDNH£Ω90°„£¨
°ý°œDHN£Ω90°„£¨
°ýBE°ÕDG£ª
£®2£©»ÁÕº£¨µ±µ„G‘⁄œþ∂ŒDE…œ ±£¨¡¨Ω”BD£¨

°þÀƒ±þ–ŒABCD «’˝∑Ω–Œ£¨Àƒ±þ–ŒAEFG «’˝∑Ω–Œ£¨
°ýAG£ΩAE£¨AB£ΩAD£Ω10£¨°œGAE£Ω°œDAB£Ω90°„£¨°œADB£Ω45°„£Ω°œABD£¨BD£Ω![]() AB£Ω10
AB£Ω10![]() £¨GE£Ω
£¨GE£Ω![]() AE£¨
AE£¨
°ý°œGAD£Ω°œEAB£¨
°ý°˜GAD°’°˜EAB£®SAS£©£¨
°ýBE£ΩDG£¨°œADG£Ω°œABE£Ω15°„£¨
°ý°œBDE£Ω45°„©Å15°„£Ω30°„£¨°œDBE£Ω45°„+15°„£Ω60°„£¨
°ý°œDEB£Ω90°„£¨
°ýBE£Ω![]() BD£Ω5
BD£Ω5![]() £ΩDG£¨DE£Ω
£ΩDG£¨DE£Ω![]() BE£Ω5
BE£Ω5![]() £¨
£¨
°ýGE£Ω5![]() ©Å5
©Å5![]() £¨
£¨
°ýAE£Ω![]() £Ω5
£Ω5![]() ©Å5£¨
©Å5£¨
µ±µ„E‘⁄œþ∂ŒDG…œ ±£¨

Õ¨¿Ìø…«ÛAE£Ω5![]() ©Å5£¨
©Å5£¨
π ¥∞∏Œ™£∫5![]() ©Å5£ª
©Å5£ª
£®3£©»ÁÕº£¨»Ùµ„G‘⁄œþ∂ŒDE…œ ±£¨

°þAD£Ω4![]() £¨AB£Ω4
£¨AB£Ω4![]() £¨AG£Ω4£¨AE£Ω4
£¨AG£Ω4£¨AE£Ω4![]() £¨
£¨
°ýDB£Ω![]() £Ω
£Ω![]() £Ω8
£Ω8![]() £¨GE£Ω
£¨GE£Ω![]() £Ω
£Ω![]() £Ω8£¨°œDAB£Ω°œGAE£Ω90°„£¨
£Ω8£¨°œDAB£Ω°œGAE£Ω90°„£¨
°ý°œDAG£Ω°œBAE£¨
”÷°þ![]() £¨
£¨
°ý°˜AGD°◊°˜AEB£¨
°ý![]() £¨°œDGA£Ω°œAEB£¨
£¨°œDGA£Ω°œAEB£¨
°ýBE£Ω![]() DG£¨
DG£¨
°þ°œDGA£Ω°œGAE+°œDEA£¨°œAEB£Ω°œDEB+°œAED£¨
°ý°œGAE£Ω°œDEB£Ω90°„£¨
°þDB2£ΩDE2+BE2£¨
°ý64°¡13£Ω£®DG+8£©2+3DG2£¨
°ýDG£Ω12ªÚDG£Ω©Å16£®…·»•£©£¨
°ýBE£Ω12![]() £¨
£¨
°þµ„M£¨N∑÷± «BD£¨DEµƒ÷–µ„£¨
°ýMN£Ω![]() BE£Ω6
BE£Ω6![]() £ª
£ª
»ÁÕº£¨µ±µ„E‘⁄œþ∂ŒDG…œ ±£¨

Õ¨¿Ìø…«Û£∫BE£Ω16![]() £¨
£¨
°þµ„M£¨N∑÷± «BD£¨DEµƒ÷–µ„£¨
°ýMN£Ω![]() BE£Ω8
BE£Ω8![]() £¨
£¨
◊€…œÀ˘ ˆ£∫MNŒ™6![]() ªÚ8
ªÚ8![]() £¨
£¨
π ¥∞∏Œ™£∫6![]() ªÚ8
ªÚ8![]() £Æ
£Æ

 »´≥ÃΩæÌœµ¡–¥∞∏
»´≥ÃΩæÌœµ¡–¥∞∏ øÏ¿÷5º”2ΩæÌœµ¡–¥∞∏
øÏ¿÷5º”2ΩæÌœµ¡–¥∞∏°æƒø°øƒ≥ƒÍº∂π≤”–150√˚≈Æ…˙£¨Œ™¡ÀΩ‚∏√–£≈Æ…˙ µ–ƒ«Ú≥…º®£®µ•Œª£∫√◊£©∫Õ—ˆŒ‘∆◊¯£®µ•Œª£∫∏ˆ£©µƒ«Èøˆ£¨¥”÷–Àʪ˙≥È»°30√˚≈Æ…˙Ω¯––≤‚ ‘£¨ªÒµ√¡ÀÀ˝√«µƒœýπÿ≥…º®£¨≤¢∂‘ ˝æðΩ¯––’˚¿Ì°¢√Ë ˆ∫Õ∑÷Œˆ£¨œ¬√Ê∏¯≥ˆ¡À≤ø∑÷–≈œ¢£Æ
![]() £Æ µ–ƒ«Ú≥…º®µƒ∆µ ˝∑÷≤º±Ì»Áœ¬£∫
£Æ µ–ƒ«Ú≥…º®µƒ∆µ ˝∑÷≤º±Ì»Áœ¬£∫
∑÷◊È | 6£Æ2°Ð | 6£Æ6°Ð | 7£Æ0°Ð | 7£Æ4°Ð | 7£Æ8°Ð | 8£Æ2°Ð |
∆µ ˝ | 2 |
| 10 | 6 | 2 | 1 |
![]() £Æ µ–ƒ«Ú≥…º®‘⁄7£Æ0°Ð
£Æ µ–ƒ«Ú≥…º®‘⁄7£Æ0°Ð![]() £º7£Æ4£Æ’‚◊ȵƒ «£∫
£º7£Æ4£Æ’‚◊ȵƒ «£∫
7.0 | 7.0 | 7.0 | 7.1 7.1 | 7.1 | 7.2 | 7.2 | 7.3 | 7.3 |
![]() £Æ“ª∑÷÷”—ˆŒ‘∆◊¯≥…º®»ÁÕºÀ˘ æ£∫
£Æ“ª∑÷÷”—ˆŒ‘∆◊¯≥…º®»ÁÕºÀ˘ æ£∫

∏˘æð“‘…œ–≈œ¢£¨ªÿ¥œ¬¡–Œ £∫
£®1£©¢Ÿ±Ì÷–mµƒ÷µŒ™ £ª
¢⁄≥È»°—ß…˙“ª∑÷÷”—ˆŒ‘∆◊¯≥…º®µƒ÷–Œª ˝Œ™ ∏ˆ£ª
£®2£©»Ù µ–ƒ«Ú≥…º®¥ÔµΩ7£Æ2√◊º∞“‘…œ£¨≥…º®º«Œ™”≈–„£¨«Îπ¿º∆»´ƒÍº∂≈Æ…˙≥…º®¥ÔµΩ”≈–„µƒ»À ˝£Æ
£®3£©∏√ƒÍº∂ƒ≥∞ýÔ˝ŒØ‘±Ω´±æ∞ý‘⁄’‚¥Œ≥È—˘≤‚ ‘÷–±ª≥È»°µƒ8√˚≈Æ…˙µƒ¡ΩœÓ≥…º®µƒ ˝æð≥≠¬º»Áœ¬£∫
≈Æ…˙¥˙¬Î | A | B | C | D | E | F | G | H |
µ–ƒ«Ú | 8£Æ1 | 7£Æ7 | 7£Æ5 | 7£Æ5 | 7£Æ3 | 7£Æ2 | 7£Æ0 | 6£Æ5 |
“ª∑÷÷”—ˆŒ‘∆◊¯ | * | 42 | 47 | * | 47 | 52 | * | 49 |
∆‰÷–”–2√˚≈Æ…˙µƒ“ª∑÷÷”—ˆŒ‘∆◊¯≥…º®Œ¥≥≠¬ºÕÍ’˚£¨µ±¿œ ¶Àµ’‚8√˚≈Æ…˙«°∫√”–4»À¡ΩœÓ≤‚ ‘≥…º®∂º¥ÔµΩ¡À”≈–„£¨”⁄ «Ã”˝ŒØ‘±Õ∆≤‚≈Æ…˙Eµƒ“ª∑÷÷”—ˆŒ‘∆◊¯≥…º®¥ÔµΩ¡À”≈–„£¨ƒ„Õ¨“‚Ô˝ŒØ‘±µƒÀµ∑®¬£ø≤¢Àµ√˜ƒ„µƒ¿Ì”…£Æ