题目内容
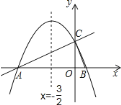
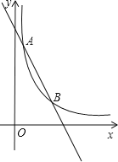
【题目】如图,已知反比例函数![]() 的图象与一次函数y=kx+b的图象交于点A(1,m),B (n,2)两点
的图象与一次函数y=kx+b的图象交于点A(1,m),B (n,2)两点
(1)求一次函数的解析式;
(2)直接写出不等式![]() ≥kx+b的解集;
≥kx+b的解集;
【答案】(1)y=-2x+8;(2)0<x≤1或x≥3;
【解析】
(1)将A、B坐标分别代入反比例函数解析式,求出m、n的值,再将求出的A、B坐标分别代入y=kx+b,求出k、b,最后得到一次函数解析式;(2)直接解不等式即可.
(1)把点A(1,m),B(n,2)分别代入y=![]() 得m=6,2n=6,解得n=3,
得m=6,2n=6,解得n=3,
∴A点坐标为(1,6),B点坐标为(3,2),
把A(1,6),B(3,2)分别代入y=kx+b得
k+b=6,3k+b=2,解得k=2,b=8,
∴一次函数解析式为y=-2x+8;
(2)![]() ≥kx+b的解集是:0<x≤1或x≥3.
≥kx+b的解集是:0<x≤1或x≥3.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?