题目内容
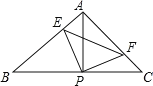
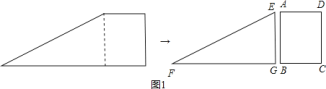
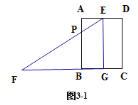
【题目】如图![]() .小明将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得
.小明将一张直角梯形纸片沿虚线剪开,得到矩形和三角形两张纸片,测得![]() ,
,![]() .在进行如下操作时遇到了下面的几个问题,请你帮助解决.
.在进行如下操作时遇到了下面的几个问题,请你帮助解决.
(1)将![]() 的顶点
的顶点![]() 移到矩形的顶点
移到矩形的顶点![]() 处,再将三角形绕点
处,再将三角形绕点![]() 顺时针旋转使
顺时针旋转使![]() 点落在
点落在![]() 边上,此时,
边上,此时,![]() 恰好经过点
恰好经过点![]() (如图
(如图![]() ),请你求出
),请你求出![]() 和
和![]() 的长度;
的长度;
(2)在(1)的条件下,小明先将三角形的边![]() 和矩形边
和矩形边![]() 重合,然后将
重合,然后将![]() 沿直线
沿直线![]() 向右平移,至
向右平移,至![]() 点与
点与![]() 重合时停止.在平移过程中,设
重合时停止.在平移过程中,设![]() 点平移的距离为
点平移的距离为![]() ,两纸片重叠部分面积为
,两纸片重叠部分面积为![]() ,求在平移的整个过程中,
,求在平移的整个过程中,![]() 与
与![]() 的函数关系式,并求当重叠部分面积为
的函数关系式,并求当重叠部分面积为![]() 时,平移距离
时,平移距离![]() 的值(如图
的值(如图![]() ).
).
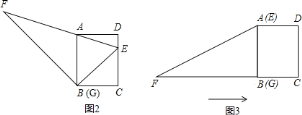
【答案】(1)![]() ,
,![]() ;(2)分两种情况:①重叠部分
;(2)分两种情况:①重叠部分![]() ,②
,②![]() ;当
;当![]() 时,
时,![]() 或
或![]() .
.
【解析】
(1)先在Rt△BCE中,利用勾股定理求得CE的长,即可得DE的长,然后在Rt△ADE中,利用勾股定理即可求得AE的长;然后根据等腰三角形的性质与互余求得![]() ,
,
则可证![]() ,即
,即![]() ,将各边数值代入即可求解;
,将各边数值代入即可求解;
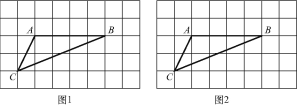
(2)如图,分x≤4与x>4两种情况,在Rt△EFG中,求得tan∠F的值,从而得到PB关于x的代数式,第一种情况根据梯形的面积公式整理即可得解;第二种情况根据y为△RPQ的面积加上矩形BCQP的面积即可得到;然后将y=10时分别代入求解即可.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,
∴![]() ,
,
则![]() ,
,
∴![]() ;
;
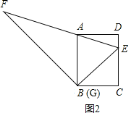
(2)分两种情况:
①是![]() ≤
≤![]() 时,如图
时,如图![]() ,
,![]() 与
与![]() 相交于
相交于![]() ,
,
∵![]() 的直角边
的直角边![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是直角梯形,
是直角梯形,
则重叠部分![]() ;
;

②是![]() >
>![]() 时,如图
时,如图![]() ,
,![]() 与
与![]() 相交于
相交于![]() ,与
,与![]() 相交于
相交于![]() ,作PQ⊥CD与Q,
,作PQ⊥CD与Q,
∵PQ∥FG,
∴∠RPQ=∠F,即tan∠RPQ=tan∠F=![]() ,
,
∴RQ=![]() PQ=2,
PQ=2,
∴![]() ,
,
当重叠部分面积为![]() 时,即
时,即![]() 分别代入两等式,
分别代入两等式,
![]() ,
,
解得:![]() (不合题意舍去)或
(不合题意舍去)或![]() ,
,
![]() 得出,
得出,![]() ,
,
∴当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() 或
或![]() .
.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目