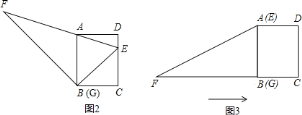Question

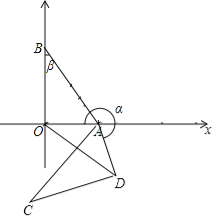
【题目】在平面直角坐标系中，己知O为坐标原点，点A（3，0），B（0.4），以点A为旋转中心，把△ABO顺时针旋转，得△ACD．记旋转角为α．∠ABO为β．

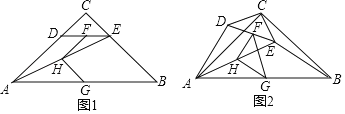
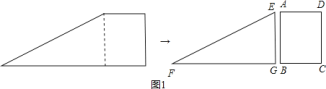
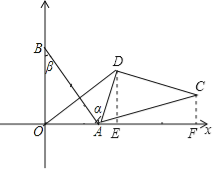
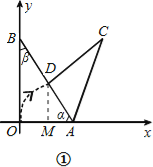
（I ）如图①，当旋转后点D恰好落在AB边上时，求点D的坐标；

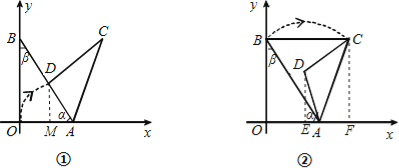
（II）如图②，当旋转后满足BC∥x轴时，求α与β之间的数量关系：

（III）当旋转后满足∠AOD=β时，求直线CD的解析式（直接写出结果即可）．

Answer 1

【答案】（1）（，） （2）α=2β （3）y=x﹣4

【解析】

试题（1）∵点A（3，0），B（0，4），得OA=3，OB=4，

∴在Rt△AOB中，由勾股定理，得AB==5，

根据题意，有DA=OA=3．

如图①，过点D作DM⊥x轴于点M，

则MD∥OB，

∴△ADM∽△ABO．有，

得，

∴OM=，

∴，

∴点D的坐标为（，）．

（2）如图②，由已知，得∠CAB=α，AC=AB，

∴∠ABC=∠ACB，

∴在△ABC中，

∴α=180°﹣2∠ABC，

∵BC∥x轴，得∠OBC=90°，

∴∠ABC=90°﹣∠ABO=90°﹣β，

∴α=2β；

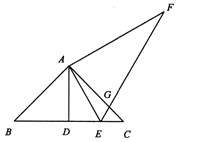
（3）若顺时针旋转，如图，过点D作DE⊥OA于E，过点C作CF⊥OA于F，

∵∠AOD=∠ABO=β，

∴tan∠AOD==，

设DE=3x，OE=4x，

则AE=4x﹣3，

在Rt△ADE中，AD2=AE2+DE2，

∴9=9x2+（4x﹣3）2，

∴x=，

∴D（，），

∴直线AD的解析式为：y=x﹣，

∵直线CD与直线AD垂直，且过点D，

∴设y=﹣x+b，把D（，）代入得，=﹣×+b，

解得b=4，

∵互相垂直的两条直线的斜率的积等于﹣1，

∴直线CD的解析式为y=﹣．

同理可得直线CD的另一个解析式为y=x﹣4．