题目内容
 如图,已知在等腰梯形ABCD中,AD∥BC,∠ABC=45°,两腰的和为8cm,点E,F分别是对角线AC,BD的中点,点G是底边BC的中点,则EF的长为
如图,已知在等腰梯形ABCD中,AD∥BC,∠ABC=45°,两腰的和为8cm,点E,F分别是对角线AC,BD的中点,点G是底边BC的中点,则EF的长为
- A.4
 cm
cm - B.2
 cm
cm - C.
 cm
cm - D.无法确定
B
分析:根据等腰梯形的性质可得∠ABC=∠ACB=45°,AB=DC=4cm,然后判断FG是△BCD的中位线,EG是△CAB的中位线,根据中位线的性质可得∠FGB=45°,∠EGC=45°,继而得出△EFG是等腰直角三角形,继而可求出EF的长度.
解答:∵四边形ABCD是等腰梯形,
∴∠ABC=∠ACB=45°,AB=DC,
又∵两腰的和为8cm,
∴AB=CD=4cm,
∵点E,F分别是对角线AC,BD的中点,点G是底边BC的中点,
∴FG是△BCD的中位线,EG是△CAB的中位线,
∴FG∥CD,FG= CD=2cm,EG∥AB,EG=
CD=2cm,EG∥AB,EG= AB=2cm,
AB=2cm,
∴∠FGB=45°,∠EGC=45°,
∴∠EFG=90°,
∴△EFG是等腰直角三角形,
∴EF= =2
=2 cm.
cm.
故选B.
点评:本题考查了三角形的中位线定理及等腰梯形的性质,解答本题的需要掌握:等腰梯形的对角线相等、同一底边上的底角相等.
分析:根据等腰梯形的性质可得∠ABC=∠ACB=45°,AB=DC=4cm,然后判断FG是△BCD的中位线,EG是△CAB的中位线,根据中位线的性质可得∠FGB=45°,∠EGC=45°,继而得出△EFG是等腰直角三角形,继而可求出EF的长度.
解答:∵四边形ABCD是等腰梯形,
∴∠ABC=∠ACB=45°,AB=DC,
又∵两腰的和为8cm,
∴AB=CD=4cm,
∵点E,F分别是对角线AC,BD的中点,点G是底边BC的中点,
∴FG是△BCD的中位线,EG是△CAB的中位线,
∴FG∥CD,FG=
 CD=2cm,EG∥AB,EG=
CD=2cm,EG∥AB,EG= AB=2cm,
AB=2cm,∴∠FGB=45°,∠EGC=45°,
∴∠EFG=90°,
∴△EFG是等腰直角三角形,
∴EF=
 =2
=2 cm.
cm.故选B.
点评:本题考查了三角形的中位线定理及等腰梯形的性质,解答本题的需要掌握:等腰梯形的对角线相等、同一底边上的底角相等.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 如图,已知在等腰梯形ABCD中,AB∥CD,AB<CD,AB=10,BC=3.
如图,已知在等腰梯形ABCD中,AB∥CD,AB<CD,AB=10,BC=3.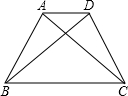 如图,已知在等腰梯形ABCD中,AD∥BC.
如图,已知在等腰梯形ABCD中,AD∥BC. 如图,已知在等腰梯形ABCD中,AD∥BC,PA=PD,问PB与PC相等吗?为什么?
如图,已知在等腰梯形ABCD中,AD∥BC,PA=PD,问PB与PC相等吗?为什么? 如图,已知在等腰梯形ABCD中,CD∥AB,AD=BC,四边形AEBC是平行四边形.求证:∠ABD=∠ABE.
如图,已知在等腰梯形ABCD中,CD∥AB,AD=BC,四边形AEBC是平行四边形.求证:∠ABD=∠ABE.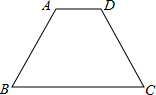 如图,已知在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=4,BC=7,求梯形ABCD的周长.
如图,已知在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=4,BC=7,求梯形ABCD的周长.