题目内容
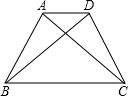 如图,已知在等腰梯形ABCD中,AD∥BC.
如图,已知在等腰梯形ABCD中,AD∥BC.(1)若AD=5,BC=11,梯形的高是4,求梯形的周长;
(2)若AD=a,BC=b,梯形的高是h,梯形的周长为c.则c=
(请用含a、b、h的代数式表示;答案直接写在横线上,不要求证明.)
(3)若AD=3,BC=7,BD=5
| 2 |
分析:(1)可过A,D两点引BC的垂线,然后根据两底的差和高的值,求出AB,CD两边,然后再得出梯形的周长;
(2)由(1)的解题过程即可得出a,b,h和c的关系式;
(3)由全等三角形ACB和DBC不难得出∠DBC=∠ACB,那么要证AC⊥DB,就要先求出∠DBC=45°,辅助线的方法同(1)过A作AE⊥BC于E,过D作DF⊥BC于F,得出BE=CF=2后即可得出BF,CE的长,然后在直角三角形DBF中可根据BD,BF的长来证得∠DBC是45°,进而可得出AC⊥DB的结论.
(2)由(1)的解题过程即可得出a,b,h和c的关系式;
(3)由全等三角形ACB和DBC不难得出∠DBC=∠ACB,那么要证AC⊥DB,就要先求出∠DBC=45°,辅助线的方法同(1)过A作AE⊥BC于E,过D作DF⊥BC于F,得出BE=CF=2后即可得出BF,CE的长,然后在直角三角形DBF中可根据BD,BF的长来证得∠DBC是45°,进而可得出AC⊥DB的结论.
解答: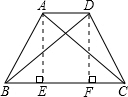 解:(1)过A作AE⊥BC于E,过D作DF⊥BC于F.则四边形ADFE是矩形.
解:(1)过A作AE⊥BC于E,过D作DF⊥BC于F.则四边形ADFE是矩形.
∵四边形ABCD是等腰梯形,且AB,CD是腰,
∴∠B=∠C,AB=CD.
∵∠AEB=∠DFC,
∴△ABE≌△CDF.
∴BE=CF=
=3.
∴直角三角形ABE中,BE=3,AE=4.
根据勾股定理可得出AB=5.
∴四边形ABCD的周长是AD+BC+2AB=26.
(2)c=2
+a+b;
(3)过A作AE⊥BC于E,过D作DF⊥BC于F.则四边形ADFE是矩形.
根据(1)可得出BE=CF=
=2,
∴BF=CE=2+3=5.
直角三角形BFD中,BD=5
,BF=5,∴cos∠DBF=
=
.
∴∠DBF=45°,同理可得:∠ACE=45°.
∴AC⊥BD.
 解:(1)过A作AE⊥BC于E,过D作DF⊥BC于F.则四边形ADFE是矩形.
解:(1)过A作AE⊥BC于E,过D作DF⊥BC于F.则四边形ADFE是矩形.∵四边形ABCD是等腰梯形,且AB,CD是腰,
∴∠B=∠C,AB=CD.
∵∠AEB=∠DFC,
∴△ABE≌△CDF.
∴BE=CF=
| BC-AD |
| 2 |
∴直角三角形ABE中,BE=3,AE=4.
根据勾股定理可得出AB=5.
∴四边形ABCD的周长是AD+BC+2AB=26.
(2)c=2
(
|
(3)过A作AE⊥BC于E,过D作DF⊥BC于F.则四边形ADFE是矩形.
根据(1)可得出BE=CF=
| BC-AD |
| 2 |
∴BF=CE=2+3=5.
直角三角形BFD中,BD=5
| 2 |
| BF |
| BD |
| ||
| 2 |
∴∠DBF=45°,同理可得:∠ACE=45°.
∴AC⊥BD.
点评:本题主要考查等腰梯形的性质的应用.

练习册系列答案
相关题目
 如图,已知在等腰梯形ABCD中,AB∥CD,AB<CD,AB=10,BC=3.
如图,已知在等腰梯形ABCD中,AB∥CD,AB<CD,AB=10,BC=3.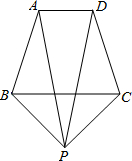 如图,已知在等腰梯形ABCD中,AD∥BC,PA=PD,问PB与PC相等吗?为什么?
如图,已知在等腰梯形ABCD中,AD∥BC,PA=PD,问PB与PC相等吗?为什么?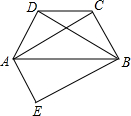 如图,已知在等腰梯形ABCD中,CD∥AB,AD=BC,四边形AEBC是平行四边形.求证:∠ABD=∠ABE.
如图,已知在等腰梯形ABCD中,CD∥AB,AD=BC,四边形AEBC是平行四边形.求证:∠ABD=∠ABE.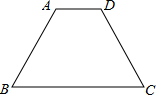 如图,已知在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=4,BC=7,求梯形ABCD的周长.
如图,已知在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=4,BC=7,求梯形ABCD的周长.