题目内容
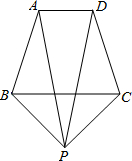 如图,已知在等腰梯形ABCD中,AD∥BC,PA=PD,问PB与PC相等吗?为什么?
如图,已知在等腰梯形ABCD中,AD∥BC,PA=PD,问PB与PC相等吗?为什么?分析:根据等腰梯形,可以得到AB=DC,∠BAD=∠CDA,结合题意条件可判断△PAB≌△PDC,从而得出PB=PC的结论.
解答:解:PB和PC相等.理由如下:
∵ABCD是等腰梯形,
∴AB=DC,∠BAD=∠CDA,
又∵PA=PD,
∴∠PAD=∠PDA.
∵∠PAB=∠BAD-∠PAD,∠PDC=∠CDA-∠PDA,
∴∠PAB=∠PDC,
在△PAB和△PDC中,
,
∴△PAB≌△PDC(SAS),
∴PB=PC.
∵ABCD是等腰梯形,
∴AB=DC,∠BAD=∠CDA,
又∵PA=PD,
∴∠PAD=∠PDA.
∵∠PAB=∠BAD-∠PAD,∠PDC=∠CDA-∠PDA,
∴∠PAB=∠PDC,
在△PAB和△PDC中,
|
∴△PAB≌△PDC(SAS),
∴PB=PC.
点评:此题考查了等腰梯形的性质、全等三角形的判定与性质,关键在于用好等腰梯形的性质,得出三角形全等的条件,从而得出全等三角形的对应边相等.

练习册系列答案
相关题目
 如图,已知在等腰梯形ABCD中,AB∥CD,AB<CD,AB=10,BC=3.
如图,已知在等腰梯形ABCD中,AB∥CD,AB<CD,AB=10,BC=3.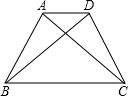 如图,已知在等腰梯形ABCD中,AD∥BC.
如图,已知在等腰梯形ABCD中,AD∥BC.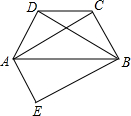 如图,已知在等腰梯形ABCD中,CD∥AB,AD=BC,四边形AEBC是平行四边形.求证:∠ABD=∠ABE.
如图,已知在等腰梯形ABCD中,CD∥AB,AD=BC,四边形AEBC是平行四边形.求证:∠ABD=∠ABE.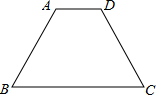 如图,已知在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=4,BC=7,求梯形ABCD的周长.
如图,已知在等腰梯形ABCD中,AD∥BC,∠B=60°,AD=4,BC=7,求梯形ABCD的周长.