��Ŀ����
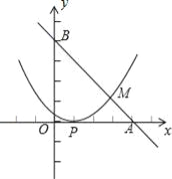
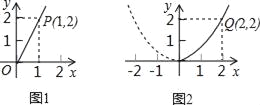
����Ŀ��ij��רҵ���ƻ�Ͷ����ֲ���ܼ���ľ�������г�������Ԥ�⣬��ֲ��ľ������y��Ͷ����x����������ϵ����ͼ1��ʾ����ֲ���ܵ�����y��Ͷ����x�ɶ��κ�����ϵ����ͼ2��ʾ��ע��������Ͷ�����ĵ�λ����Ԫ��
��1���ֱ��������y1��y2����Ͷ����x�ĺ�����ϵʽ��
��2�������λרҵ����8��Ԫ�ʽ�Ͷ����ֲ���ܺ���ľ�������ٻ�ö����������ܻ�ȡ����������Ƕ��٣�
��3���ڣ�2���Ļ�����Ҫ��֤������22��Ԫ���ϣ�����רҵ��Ӧ����Ͷ�ʣ�
���𰸡�(1)y1=2x,y2=![]() x2��x��0����(2) x=8ʱ��w�����ֵ��32 ;(3)������.
x2��x��0����(2) x=8ʱ��w�����ֵ��32 ;(3)������.
��������
��1���ɸ���ͼ�����ô���ϵ������⺯������ʽ��
��2������������=��ľ����+���������г�������ϵʽ������������ֵ��
��3����w=22���x��ֵ���ɵã�
��1����y1=kx����ͼ1��ʾ������y1=kx��ͼ�����1��2����
����2=k1��k=2��
������y1����Ͷ����x�ĺ�����ϵʽ��y1=2x��x��0����
�߸������ߵĶ�����ԭ�㣬
����y2=ax2��
��ͼ2��ʾ������y2=ax2��ͼ�����2��2����
��2=a22��
��ã�a=![]() ��
��
������y2����Ͷ����x�ĺ�����ϵʽ�ǣ�y=![]() x2��x��0����
x2��x��0����
��2����Ϊ��ֲ����x��Ԫ��0��x��8������Ͷ����ֲ��ľ��8��x����Ԫ��
w=2��8��x��+0.5 x2=![]() x2��2x+16=
x2��2x+16=![]() ��x��2��2+14��
��x��2��2+14��
��a=0.5��0��0��x��8��
�൱x=2ʱ��w����Сֵ��14��
��a=0.5��0��
�൱x��2ʱ��w��x�������������
��0��x��8��
�൱ x=8ʱ��w�����ֵ��32��
��3���������⣬��w=22ʱ��![]() ��x��2��2+14=22��
��x��2��2+14=22��
��ã�x=��2���ᣩ��x=6��
��w=![]() ��x��2��2+14��2��x��8�ķ�Χ����x������w����
��x��2��2+14��2��x��8�ķ�Χ����x������w����
��w��22��ֻ��Ҫx��6��
�ʱ�֤������22��Ԫ���ϣ�����רҵ��ӦͶ�ʳ���6��Ԫ��