题目内容
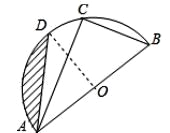
【题目】已知:如图,AB为半圆O的直径,C、D是半圆O上的两点,若直径AB的长为4,且BC=2,∠DAC=15°.
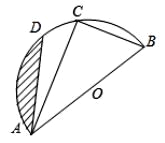
(1)求∠DAB的度数;
(2)求图中阴影部分的面积(结果保留π)
【答案】(1)45°;(2)π-2.
【解析】
(1)根据含30°角的直角三角形性质求出∠CAB,即可得出答案;
(2)连接OD,求出∠DOA,分别求出扇形AOD和△AOD面积,即可得出答案.
(1)解:∵AB 是直径∴∠ACB=90°,
又∵BC=2,AB=4,
∴ BC= ![]() ,
,
∴∠BAC=30°,
∴∠DAB=∠DAC+∠BAC=15°+30°=45°;
(2)解:连接 OD,
∵直径 AB=4,
∴半径 OD=OA=2,
∵OA=OD,∠DAB=45°,
∴∠ADO=∠DAB=45°,
∴∠AOD=90°,
∴阴影部分的面积S=S扇形AOD-S△AOD=![]() .
.

练习册系列答案
相关题目