Question

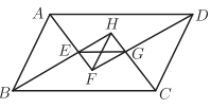
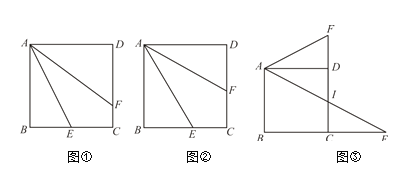
【题目】如图，在四边形ABCD中，∠ABC＝∠BCD＝90°，点E为BC的中点，AE⊥DE．

（1）求证：△ABE∽△ECD；

（2）求证：AE2＝AB·AD；

（3）若AB＝1，CD＝4，求线段AD，DE的长．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）10.

【解析】试题分析：（1）根据垂直的定义和直角三角形的性质，求出∠BAE=∠CED，然后利用两角对应相等的两三角形相似可证；

（2）根据相似三角形的性质：相似三角形的对应边成比例，以及两边对应成比例且夹角相等的两三角形相似，可证明结论；

（3）根据相似三角形的性质，由（2）的结论△ABE∽△AED得到对应边成比例，然后根据勾股定理求解.

试题解析：(1)证明：∵AE⊥DE，∴∠AED＝90°，∴∠AEB+∠CED=180°-90°=90°，

∵∠ABC＝90°，∴∠BAE+∠AEB=90°，∴∠BAE=∠CED.

又∵∠ABC＝∠BCD，∴△ABE∽△ECD．

(2) ∵△ABE∽△ECD，∴ ．

∵点E为BC的中点，∴BE＝EC．

∴．

又∵∠ABC＝∠AED＝90°，∴△ABE∽△AED，

∴，∴AE2＝AB·AD．

(3)∵△ABE∽△ECD，∴ ．

∵AB＝1，CD＝4，BE＝EC，∴BE2＝AB·CD＝4．

由勾股定理，得AE2＝AB2+ BE2=5．

∵AE2＝AB·AD，∴．

由勾股定理，得．