题目内容
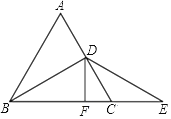
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,

(1)求证:DB=DE
(2)在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
【答案】(1)证明见解析;(2)48.
【解析】
(1)根据△ABC是等边三角形,BD是中线,可知∠DBC=30°,由CE=CD,∠ACD=60°可求得∠DCE=30°,即∠DBC=∠DCE,则DB=DE;
(2)根据Rt△DCF中∠FCD=30°知CD=2CF=4,即可知AC=8,则可求出△ABC的周长.
(1)解:证明:∵△ABC是等边三角形,BD是中线,
∴∠ABC=∠ACB=60°.
∠DBC=30°(等腰三角形三线合一).
又∵CE=CD,
∴∠CDE=∠CED.
又∵∠BCD=∠CDE+∠CED,
∴∠CDE=∠CED= ![]() ∠BCD=30°.
∠BCD=30°.
∴∠DBC=∠DEC.
∴DB=DE(等角对等边);
(2)解: ∵∠CDE=∠CED= ![]() ∠BCD=30°,DF⊥BE.
∠BCD=30°,DF⊥BE.
∴∠CDF=30°,
∵CF=4,
∴DC=8,
∵AD=CD,
∴AC=16,
∴△ABC的周长=3AC=48.

练习册系列答案
相关题目