题目内容
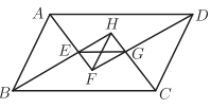
【题目】如图,平行四边形ABCD的四个内角的平分线相交成四边形EFGH,求证:
(1)EG=HF.
(2)EG=BC-AB.
【答案】(1)见详解;(2)见详解.
【解析】
(1)利用三个内角等于90°的四边形是矩形,即可证明;
(2)延长AF交BC于M,通过全等得到AB=BM,然后证明四边形EMCG是平行四边形,得到EG=CM,即可得证.
解:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵BH,CH分别平分∠ABC与∠BCD,
∴∠HBC=![]() ∠ABC,∠HCB=
∠ABC,∠HCB=![]() ∠BCD,
∠BCD,
∴∠HBC+∠HCB=![]() (∠ABC+∠BCD)=
(∠ABC+∠BCD)=![]() ×180°=90°,
×180°=90°,
∴∠H=90°,
同理∠HEF=∠F=90°,
∴四边形EFGH是矩形,
∴EG=HF;
(2)如图,延长AF交BC于M,
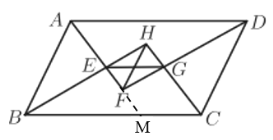
由(1)中可知AE⊥AF,即∠BEA=∠BEM=90°,
在Rt△ABE和Rt△MBE中,
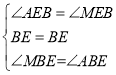 ,
,
∴△ABE≌△MBE,
∴AB=MB,AE=EM,
由于四边形ABCD是平行四边形,
∴∠ABC=∠ADC,AB=CD
∵BH,DF分别平分∠ABC与∠ADC,
∴∠ABE=∠CDG,
在Rt△ABE和Rt△CDG中,
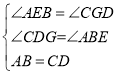 ,
,
∴△ABE≌△CDG,
∴CG=AE,
∴CG=EM,
由于四边形EFGH是矩形,
∴EM∥CG,
∴四边形EMCG是平行四边形,
∴EG=MC,
由于MC=BC-BM,
∴EG=BC-AB.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目