题目内容
【题目】如图,已知四边形DFBE是矩形,C,A分别是DF,BE延长线上的点, ![]() , 求证:
, 求证:
(1)AE=CF.
(2)四边形ABCD是平行四边形.
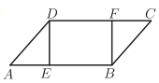
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)由矩形的性质得出∠DEB=∠BFD=90°,DE=BF,故∠DEA=∠BFC,由ASA证明△ADE≌△CBF即可得出结论;
(2)由△ADE≌△CBF可得∠DAE=∠BCF,由矩形的性质得出∠EDF=∠ABF=90°可得∠ADC=∠ABC,即可得出结论.
(1)在矩形DFBE中,∠DEB=∠BFD=90°,DE=BF
∵∠AED+∠DEB=180°,∠CFB+∠BFD=180°
∴∠AED=∠CFB=90°
又∵∠ADE=∠CBF
∴△ADE≌△CBF
∴AE=CF
(2)∵△ADE≌△CBF
∴∠A=∠C
∵在矩形DFBE中,∠EDF=∠FBA=90°
∴∠EDF+∠ADE=∠FBA+∠CBF
即∠ADC=∠ABC
又∵∠A=∠C
∴四边形ABCD是平行四边形

练习册系列答案
相关题目