题目内容
【题目】在正方形ABCD中,点E是射线BC上的点,直线AF与直线AB关于直线AE对称,直线AF交射线CD于点F.
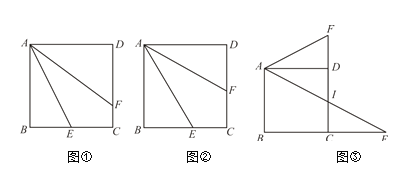
(1)如图①,当点E是线段BC的中点时,求证:AF=AB+CF;
(2)如图②,当∠BAE=30°时,求证:AF=2AB﹣2CF;
(3)如图③,当∠BAE=60°时,(2)中的结论是否还成立?若不成立,请判断AF与AB、CF之间的数量关系,并加以证明.
【答案】(1)证明见解析;(2)证明见解析;(3)成立,理由见解析
【解析】
(1)由折叠的性质得出AG=AB,BE=GE,进而用HL判断出Rt△EGF≌Rt△ECF,代换即可得出结论;
(2)利用含30°的直角三角形的性质即可证明;
(3)先判断出△AIF为等边三角形,得出AI=FI=AF,再代换即可得出结论.
(1)如图,过点E作EG⊥AF于点G,连接EF.
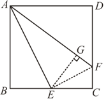
由折叠性质知,△ABE≌△AGE,
∴AG=AB,BE=GE,
∵BE=CE,
∴GE=CE,
在Rt△EGF和Rt△ECF中,
![]() ,
,
∴Rt△EGF≌Rt△ECF,(HL)
∴FG=FC,
∵AF=AG+FG,
∴AF=AB+FC ;
(2)如图,延长AF、BC交于点H.
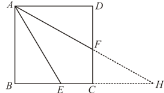
在正方形ABCD中,
∠B =90°,
由折叠性质知,∠BAE=∠HAE=30°,
∴∠H=90°-∠BAE-∠HAE =30°,
Rt△ABH中,∠B =90°,∠H =30°,
∴AH=2AB,
同理:FH=2FC,
∵AF=AH﹣FH,
∴AF=2AB﹣2FC;
(3)由折叠知,∠BAE=∠FAE=60°,
∴∠DAE=∠DAF=30°,
又∵AD⊥IF,
∴△AIF为等边三角形,
∴AF=AI=FI,
由(2)可得AE=2AB,
IE=2IC,
∵IC=FC-FI,
∴IC=FC-AF,
∴IE=2FC-2AF,
∵AI=AE-IE,
∴AF=2AB-(2FC-2AF)
=2FC-2AB.

 科学实验活动册系列答案
科学实验活动册系列答案