题目内容
已知关于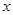 的一元二次方程
的一元二次方程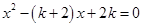 .
.
(1)试说明无论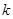 取何值时,这个方程一定有实数根;
取何值时,这个方程一定有实数根;
(2)已知等腰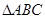 的一边
的一边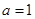 ,若另两边
,若另两边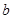 、
、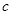 恰好是这个方程的两个根,求
恰好是这个方程的两个根,求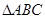 的周长.
的周长.
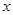 的一元二次方程
的一元二次方程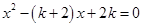 .
.(1)试说明无论
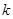 取何值时,这个方程一定有实数根;
取何值时,这个方程一定有实数根;(2)已知等腰
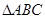 的一边
的一边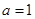 ,若另两边
,若另两边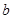 、
、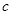 恰好是这个方程的两个根,求
恰好是这个方程的两个根,求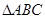 的周长.
的周长.(1)证明见解析;(2)5.
试题分析:(1)先计算△=(k+2)2-4×2k,根据非负数的性质得到△≥0,然后根据△的意义即可得到结论;
(2)先解出原方程的解为x1=k,x2=2,然后分类讨论:腰长为5时,则k=5;当底边为5时,则x1=x2,得到k=8,然后分别计算三角形的周长.
试题解析:(1)∵△=(k+2)2-4×2k=(k-2)2,
∵(k-2)2,≥0,
∴△≥0,
∴无论k取任何实数,方程总有实数根;
(2)解方程x2-(k+2)x+2k=0得x1=k,x2=2,
①当腰长为1时,等腰三角形不存在;
②当底边为1时,
∴x1=x2,
∴k=2,
∴周长=2+2+1=5.
考点: 1.根与系数的关系;2.根的判别式;3.等腰三角形的性质.

练习册系列答案
相关题目
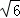 x+3=0;
x+3=0;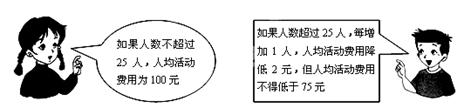 春游活动结束后,该班共支付给该旅行社活动费用2800元,请问该班共有多少人参加这次春游活动?
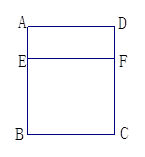
春游活动结束后,该班共支付给该旅行社活动费用2800元,请问该班共有多少人参加这次春游活动?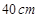 的铁丝剪成两段,并把每一段各围成一个正方形.
的铁丝剪成两段,并把每一段各围成一个正方形.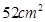 ,小林该怎么剪?
,小林该怎么剪?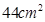 .”他的说法对吗?请说明理由.
.”他的说法对吗?请说明理由.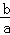 ,x1•x2=
,x1•x2=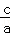 .根据该材料填空:已知x1,x2,是方程x2+6x+3=0的两实数根,则
.根据该材料填空:已知x1,x2,是方程x2+6x+3=0的两实数根,则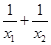 的值为 _________ .
的值为 _________ .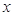
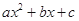
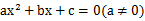 的一个解
的一个解