题目内容
已知关于x的一元二次方程x2+2(k﹣1)x+k2﹣1=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)0可能是方程的一个根吗?若是,请求出它的另一个根;若不是,请说明理由.
(1)求实数k的取值范围;
(2)0可能是方程的一个根吗?若是,请求出它的另一个根;若不是,请说明理由.
(1)k<1;(2)是,4.
试题分析:(1)方程有两个不相等的实数根,必须满足△=b2﹣4ac>0,由此可以得到关于k的不等式,然后解不等式即可求出实数k的取值范围;
(2)利用假设的方法,求出它的另一个根.
试题解析:(1)∵△=[2(k﹣1)]2﹣4(k2﹣1)=4k2﹣8k+4﹣4k2+4=﹣8k+8,
又∵原方程有两个不相等的实数根,
∴﹣8k+8>0,
解得k<1,
即实数k的取值范围是k<1;
(2)假设0是方程的一个根,
则代入原方程得02+2(k﹣1)•0+k2﹣1=0,
解得k=﹣1或k=1(舍去),
即当k=﹣1时,0就为原方程的一个根,
此时原方程变为x2﹣4x=0,
解得x1=0,x2=4,
所以它的另一个根是4.
考点: 根的判别式.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
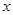 的一元二次方程
的一元二次方程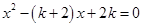 .
.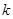 取何值时,这个方程一定有实数根;
取何值时,这个方程一定有实数根;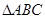 的一边
的一边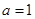 ,若另两边
,若另两边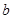 、
、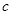 恰好是这个方程的两个根,求
恰好是这个方程的两个根,求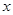 的方程
的方程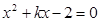
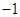 ,求另一个根及
,求另一个根及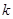 值.
值.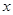 的方程中,一定是一元二次方程的为 ( )
的方程中,一定是一元二次方程的为 ( )



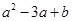 ,如:3★5=
,如:3★5=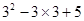 ,若x★2=6,则实数x的值是( )
,若x★2=6,则实数x的值是( ) 或
或

 是关于
是关于 的一元二次方程,则
的一元二次方程,则 的值应为( )
的值应为( ) =2
=2
