题目内容
【题目】如图，抛物线y=ax2+bx+c的图象经过点A（﹣2，0），点B（4，0），点D（2，4），与y轴交于点C，作直线BC，连接AC，CD．
（1）求抛物线的函数表达式；
（2）E是抛物线上的点，求满足∠ECD=∠ACO的点E的坐标；
（3）点M在y轴上且位于点C上方，点N在直线BC上，点P为第一象限内抛物线上一点，若以点C，M，N，P为顶点的四边形是菱形，求菱形的边长．
【答案】（1）y=﹣
x2+x+4；（2）点E的坐标为（1，
），（3，
）；（3）菱形的边长为4
﹣4．
【解析】
试题分析：（1）把点A（﹣2，0），点B（4，0），点D（2，4）代入y=ax2+bx+c，用待定系数法求出抛物线解析式即可．（2）分点E在直线CD上方的抛物线上和点E在直线CD下方的抛物线上两种情况，用三角函数求解即可；（3）分CM为菱形的边和CM为菱形的对角线两种情况，用菱形的性质进行计算即可.
试题解析：（1）∵抛物线y=ax2+bx+c的图象经过点A（﹣2，0），点B（4，0），点D（2，4），
∴设抛物线解析式为y=a（x+2）（x﹣4），
∴﹣8a=4，
∴a=﹣
，
∴抛物线解析式为y=﹣（x+2）（x﹣4）=﹣x2+x+4；
（2）如图1，
①点E在直线CD上方的抛物线上，记E′，
连接CE′，过E′作E′F′⊥CD，垂足为F′，
由（1）知，OC=4，
∵∠ACO=∠E′CF′，
∴tan∠ACO=tan∠E′CF′，
∴
=，
设线段E′F′=h，则CF′=2h，
∴点E′（2h，h+4）
∵点E′在抛物线上，
∴﹣（2h）2+2h+4=h+4，
∴h=0（舍）h=
∴E′（1，
），
②点E在直线CD下方的抛物线上，记E，
同①的方法得，E（3，
），
点E的坐标为（1，
），（3，
）
（3）①CM为菱形的边，如图2，
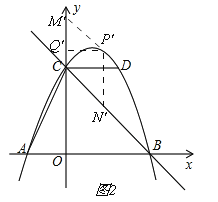
在第一象限内取点P′，过点
P′作P′N′∥y轴，交BC于N′，过点P′作P′M′∥BC，
交y轴于M′，
∴四边形CM′P′N′是平行四边形，
∵四边形CM′P′N′是菱形，
∴P′M′=P′N′，
过点P′作P′Q′⊥y轴，垂足为Q′，
∵OC=OB，∠BOC=90°，
∴∠OCB=45°，
∴∠P′M′C=45°，
设点P′（m，﹣m2+m+4），
在Rt△P′M′Q′中，P′Q′=m，P′M′=
m，
∵B（4，0），C（0，4），
∴直线BC的解析式为y=﹣x+4，
∵P′N′∥y轴，
∴N′（m，﹣m+4），
∴P′N′=﹣m2+m+4﹣（﹣m+4）=﹣m2+2m，
∴
m=﹣m2+2m，
∴m=0（舍）或m=4﹣2，
菱形CM′P′N′的边长为（4﹣2）=4
﹣4．
②CM为菱形的对角线，如图3，
在第一象限内抛物线上取点P，过点P作PM∥BC，
交y轴于点M，连接CP，过点M作MN∥CP，交BC于N，
∴四边形CPMN是平行四边形，连接PN交CM于点Q，
∵四边形CPMN是菱形，
∴PQ⊥CM，∠PCQ=∠NCQ，
∵∠OCB=45°，
∴∠NCQ=45°，
∴∠PCQ=45°，
∴∠CPQ=∠PCQ=45°，
∴PQ=CQ，
设点P（n，﹣n2+n+4），
∴CQ=n，OQ=n+2，
∴n+4=﹣n2+n+4，
∴n=0（舍），
∴此种情况不存在．
∴菱形的边长为4﹣4．
