题目内容

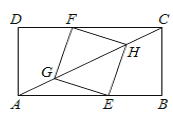
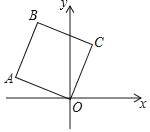
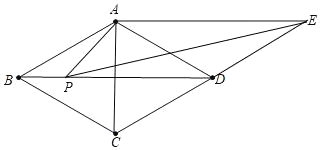
【题目】如图，EF⊥AD，将平行四边形ABCD沿着EF对折．设∠1的度数为n°，则∠C=______．（用含有n的代数式表示）

【答案】180°﹣n°

【解析】

由四边形ABCD是平行四边形，可知∠B=180°﹣∠C；再由由折叠的性质可知，∠GHC=∠C，即可得∠GHB=180°﹣∠C；根据三角形的外角的性质可知∠1=∠GHB+∠B=360°﹣2∠C，即可得360°﹣2∠C=n°，由此求得∠C=180°﹣n°.

∵四边形ABCD是平行四边形，

∴∠B=180°﹣∠C，

由折叠的性质可知，∠GHC=∠C，

∴∠GHB=180°﹣∠C，

由三角形的外角的性质可知，∠1=∠GHB+∠B=360°﹣2∠C，

∴360°﹣2∠C=n°，

解得，∠C=180°﹣n°，

故答案为：180°﹣n°．

练习册系列答案
相关题目

【题目】在矩形纸片ABCD中，AD=8，AB=6，E是边BC上的点，将纸片沿AE折叠，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为（ ）

A. 3 B. 5 C. 3或5 D. 3或6

【题目】为了解甲、乙两班英语口语水平，每班随机抽取了10名学生进行了口语测验，测验成绩满分为10分，参加测验的10名学生成绩（单位：分）称为样本数据，抽样调查过程如下：

收集数据

甲、乙两班的样本数据分别为：

甲班：6 7 9 4 6 7 6 9 6 10

乙班：7 8 9 7 5 7 8 5 9 5

整理和描述数据

规定了四个层次：9分以上（含9分）为“优秀”，8-9分（含8分）为“良好”，6-8分（含6分）为“一般”，6分以下（不含6分）为“不合格”。按以上层次分布绘制出如下的扇形统计图。

请计算：（1）图1中，“不合格”层次所占的百分比；

（2）图2中，“优秀”层次对应的圆心角的度数。

分析数据

对于甲、乙两班的样本数据，请直接回答：

（1）甲班的平均数是7，中位数是_____；乙班的平均数是_____，中位数是7；

（2）从平均数和中位数看，____班整体成绩更好。

解决问题

若甲班50人，乙班40人，通过计算，估计甲、乙两班“不合格”层次的共有多少人？

【题目】某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系，如图所示．

（1）求每位“快递小哥”的日收入y（元）与日派送量x（件）之间的函数关系式；

（2）已知某“快递小哥”的日收入不少于110元，则他至少要派送多少件？

【题目】情境观察：

如图1，△ABC中，AB=AC，∠BAC=45°，CD⊥AB，AE⊥BC，垂足分别为D、E，CD与AE交于点F．

①写出图1中所有的全等三角形 ；

②线段AF与线段CE的数量关系是 ．

问题探究：

如图2，△ABC中，∠BAC=45°，AB=BC，AD平分∠BAC，AD⊥CD，垂足为D，AD与BC交于点E．

求证：AE=2CD．

拓展延伸：

如图3，△ABC中，∠BAC=45°，AB=BC，点D在AC上，∠EDC= ∠BAC，DE⊥CE，垂足为E，DE与BC交于点F．求证：DF=2CE．

要求：请你写出辅助线的作法，并在图3中画出辅助线，不需要证明．

【题目】如图，在△ABC中，CE平分∠ACB交AB于E点，DE∥BC，DF∥AB．

（1）若∠BCE＝25°，请求出∠ADE的度数；

（2）已知：BF＝2BE，DF交CE于P点，连结BP，AB⊥BP．

①猜想：△CDF的边DF与CD的数量关系，并说明理由；

②取DE的中点N，连结NP．求证：∠ENP＝3∠DPN．

【题目】如图，矩形ABCD中，AB=8，BC=6．点E在边AB上，点F在边CD上，点G、H在对角线AC上，若四边形EGFH是菱形，则AE的长是_________________。

【题目】如图，在正方形OABC中，点A的坐标是（﹣3，1），点B的纵坐标是4，则B，C两点的坐标分别是（　　）

A. （﹣2，4），（1，3） B. （﹣2，4），（2，3）

C. （﹣3，4），（1，4） D. （﹣3，4），（1，3）

【题目】如图，在菱形ABCD中，∠ABC＝60°，AB＝2．过点A作对角线BD的平行线与边CD的延长线相交于点E．P为边BD上的一个动点（不与端点B，D重合），连接PA，PE，AC．

（1）求证：四边形ABDE是平行四边形；

（2）求四边形ABDE的周长和面积；

（3）记△ABP的周长和面积分别为C1和S1，△PDE的周长和面积分别为C2和S2，在点P的运动过程中，试探究下列两个式子的值或范围：①C1+C2，②S1+S2，如果是定值的，请直接写出这个定值；如果不是定值的，请直接写出它的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网