题目内容
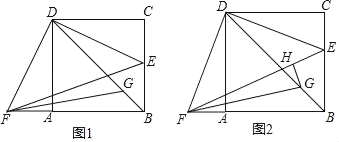
【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2.过点A作对角线BD的平行线与边CD的延长线相交于点E.P为边BD上的一个动点(不与端点B,D重合),连接PA,PE,AC.
(1)求证:四边形ABDE是平行四边形;
(2)求四边形ABDE的周长和面积;
(3)记△ABP的周长和面积分别为C1和S1,△PDE的周长和面积分别为C2和S2,在点P的运动过程中,试探究下列两个式子的值或范围:①C1+C2,②S1+S2,如果是定值的,请直接写出这个定值;如果不是定值的,请直接写出它的取值范围.
【答案】(1)见解析;(2)ABDE的周长为:![]() ,面积为
,面积为![]() ;
;
(3)①![]() ;②S1+S2的值为定值,这个定值为
;②S1+S2的值为定值,这个定值为![]()
【解析】
(1)利用菱形的性质得:AB∥DE,由两组对边分别平行的四边形可得结论;
(2)设对角线AC与BD相交于点O.根据直角三角形30°角的性质得AC的长,由勾股定理得OB的长和BD的长,根据平行四边形的性质可得其周长和面积;
(3)①先根据三角形的周长计算C1+C2=2AB+BD+AP+PE=4+2![]() +AP+PE,确定AP+PE的最大值和最小值即可;
+AP+PE,确定AP+PE的最大值和最小值即可;
根据轴对称的最短路径问题可得:当P在D处时,AP+PE的值最小,最小值是2+2=4,由图形可知:当P在点B处时,AP+PE的值最大,构建直角三角形计算即可;
②S1+S2的值为定值,这个定值为![]() ,根据面积公式可得结论.
,根据面积公式可得结论.
(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,
即AB∥DE.
∵BD∥AE,
∴四边形ABDE是平行四边形.
(2)解:设对角线AC与BD相交于点O.
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ABD=∠CBP=![]() ∠ABC=30°,AC⊥BD.
∠ABC=30°,AC⊥BD.
在Rt△AOB中,AO=![]() AB=1,
AB=1,
∴OB=![]() .
.
∴BD=2BO=2![]() .
.
∴![]() ABDE的周长为:2AB+2BD=4+4
ABDE的周长为:2AB+2BD=4+4![]() ,
,
![]() ABDE的面积为:BDAO=2
ABDE的面积为:BDAO=2![]() ×1=2
×1=2![]() .
.
(3)①∵C1+C2=AB+PB+AP+PD+PE+DE=2AB+BD+AP+PE=4+2![]() +AP+PE,
+AP+PE,
∵C和A关于直线BD对称,
∴当P在D处时,AP+PE的值最小,最小值是2+2=4,
当P在点B处时,AP+PE的值最大,如图2,
过E作EG⊥BD,交BD的延长线于G,
∵∠BDE=150°,
∴∠EDG=30°,
∵DE=2,
∴EG=1,DG=![]() ,
,
Rt△PEG中,BG=2![]() +
+![]() =3
=3![]() ,
,
由勾股定理得:PE=![]() ,
,
∴AP+PE的最大值是:2+2![]() ,
,
∵P为边BD上的一个动点(不与端点B,D重合),
∴4+4+2![]() <C1+C2<4+2
<C1+C2<4+2![]() +2+2
+2+2![]() ,即8+2
,即8+2![]() <C1+C2<6+2
<C1+C2<6+2![]() +2
+2![]() ;
;
(写对一边的范围给一分)
②S1+S2的值为定值,这个定值为![]() ;
;
理由是:S1+S2=![]() .
.



 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案