��Ŀ����
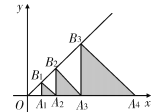
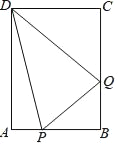
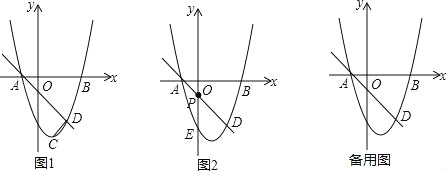
����Ŀ����ͼ1����֪������y=ax2��2ax��3��x�ύ��A��B���㣬�䶥��ΪC������A��ֱ�߽�����������һ��D��2����3������tan��BAD=1��
��1���������ߵĽ���ʽ��
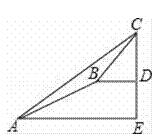
��2������CD����֤��AD��CD��
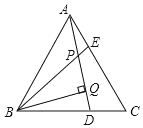
��3����ͼ2��P���߶�AD�ϵĶ��㣬����P��y���ƽ���߽��������ڵ�E�����߶�PE���ȵ����ֵ��
��4����Q���������ϵĶ��㣬��x�����Ƿ���ڵ�F��ʹ��A��D��F��QΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=x2��2x��3����2��֤������������3��![]() ����4�����ڣ�����3��0����4+
����4�����ڣ�����3��0����4+![]() ��0����4��
��0����4��![]() ��0����1��0��.
��0����1��0��.
��������
��1������D��DM��x����M�����ݵ�D���������DM��OM���ٸ��ݡ�BAD������ֵ���AM��Ȼ�����AO���Ӷ��õ���A�����꣬�ٴ��������߱���ʽ���a���Ӷ��ý⣻
��2�����������߽���ʽ�������C�����꣬�����ù��ɶ�����ʽ���AC��CD��AD��Ȼ�����ù��ɶ����涨��֤�����ɣ�
��3�����ô���ϵ�������ֱ��AD�Ľ���ʽ���ٱ�ʾ��PE��Ȼ����ݶ��κ�������ֵ������⼴�ɣ�
��4�����F������Ϊ��x��0����Ȼ��֢�AD��ƽ���ı��εı���FQ��x���·�ʱ����ʾ����Q�����꣬Ȼ����������߽���ʽ��⼴�ɣ�FQ��x���Ϸ�ʱ����ʾ����Q�����꣬�ٴ��������߽���ʽ��⣻��AD��ƽ���ı��ζԽ���ʱ������ƽ���ı��ζԱ�ƽ�пɵ�DQ��x�ᣬȻ����ݵ�D�������������Q�����꣬�ٸ���AF=DQ�����F�����꼴�ɣ�
��1����ͼ������D��DM��x����M��
��D��2����3����
��DM=3��OM=2��
��tan��BAD=1��
��AM=DM=3��
��AO=AM��OM=3��2=1��
���A����������1��0����
����A��������������ߵã�a+2a��3=0��
���a=1��
���ԣ�y=x2��2x��3��
��2��֤������y=x2��2x��3=��x��1��2��4��
�ඥ��C��1����4����
�ɹ��ɶ����ã�AD2=32+32=18��
CD2=��2��1��2+����3+4��2=2��
AC2=��1+1��2+42=20��
��AD2+CD2=AC2=20��
���ACD��ֱ�������Σ��ҡ�ADC=90�㣬
��AD��CD��
��3����ֱ��AD�Ľ���ʽΪy=kx+b��k��0����
����A��D���������ã�![]() ��
��
���![]() ��
��
���ԣ�ֱ��AD�Ľ���ʽΪy=��x��1��
���ԣ�PE=����x��1������x2��2x��3��=��x2+x+2=����x��![]() ��2+
��2+![]() ��
��
��P���߶�AD�ϵĶ��㣬
����1��x��2��
�൱x=![]() ʱ���߶�PE���ȵ����ֵ��
ʱ���߶�PE���ȵ����ֵ��![]() ��
��
��4�����F��������x��0����
��AD��ƽ���ı��εı���FQ��x���·�ʱ����Q������Ϊ��x+3����3����
���������ߵã���x+3��2��2��x+3����3=��3��
���x1=��3��x2=��1����ȥ����
���ԣ�F����3��0����
FQ��x���Ϸ�ʱ����Q������Ϊ��x��3��3����
���������ߵã���x��3��2��2��x��3����3=3��
�����ã�x2��8x+9=0��
��ã�x=4��![]() ��
��
���ԣ�F��4+![]() ��0����4��
��0����4��![]() ��0����
��0����
��AD��ƽ���ı��ζԽ���ʱ����A��F����x���ϣ�
��DQ��x�ᣬ
���Q����������3��
��x2��2x��3=��3��
���x1=2��x2=0��
��DQ=2��
��AF=2��
��AO=1��
��OF=2��1=1��
��F��1��0����
����������x���ϴ��ڵ�F����3��0����4+![]() ��0����4��
��0����4��![]() ��0����1��0����ʹ��A��D��F��QΪ������ı�����ƽ���ı��Σ�
��0����1��0����ʹ��A��D��F��QΪ������ı�����ƽ���ı��Σ�