题目内容
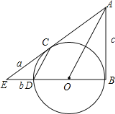
【题目】已知PA、PB是⊙O的切线,A、B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
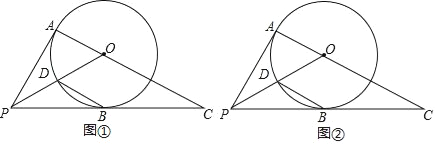
(1)如图①,若∠AOP=65°,求∠C的大小;
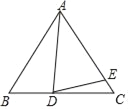
(2)如图②,连接BD,若BD∥AC,求∠C的大小.
【答案】(1)40°;(2)30°.
【解析】
(1) 连接OB,根据切线长定理可知∠APO=∠BPO=25,利用三角形的外角性质求出∠C.
(2)连接OB,先利用BD∥AC,说明△OBD是等边三角形,得出∠BOP=∠AOP=60,∠APO=30,利用三角形的外角性质求出∠C.
解:(1)连接BO,
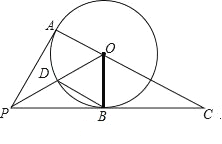
∵PA、PB是⊙O的切线,
∴∠APO=∠BPO,PA⊥AO,PB⊥OB,
∵∠AOP=65°,
∴∠APO=90°﹣65°=25°,
∴∠BPO=∠APO=25°,
∵∠AOP=∠BPO+∠C,
∴∠C=∠AOP﹣∠BPO=65°﹣25°=40°,
(2)连接OB,设∠AOP=x,

∵PA、PB是⊙O的切线,
∴∠APO=∠BPO,PA⊥AO,PB⊥OB,
∴∠AOP=∠BOP,OA=OB=OD,
∵BD∥AC,
∴∠ODB=∠AOP,
∴∠ODB=∠BOP,即∠ODB=∠BOD,
∴BD=OB=OD,
∴△OBD是等边三角形,
∴∠BOP=∠AOP=60,
∴∠BPO=30,
∴∠C=∠AOP-∠BPO=30.
故答案为:(1)40°;(2)30°.

练习册系列答案
相关题目