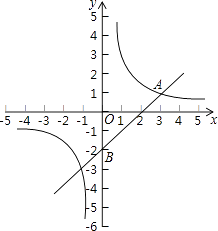题目内容
【题目】二次函数y=ax2+bx+c的图象如图所示，关于此二次函数有以下四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④ab＞0，其中正确的有（ ）个．
A.1
B.2
C.3
D.4
【答案】B
【解析】∵图象开口向下，
∴a＜0，
故①正确；
∵图象与y轴的交点坐标在x轴的下方，
∴c＜0，
故②不正确；
∵抛物线与x轴有两个交点，
∴方程ax2+bx+c=0有两个不相等的实数根，
∴b2﹣4ac＞0，
故③正确；
∵图象对称轴在y轴的右侧，
∴﹣ 
＞0，
∴ab＜0，
故④不正确；
∴正确的有两个，
故答案为：B．
①由图象开口向下得a＜0，故①正确；
②由图象与y轴的交点坐标在x轴的下方得c＜0，故②不正确；
③由抛物线与x轴有两个交点得b2﹣4ac＞0，故③正确；
由图象对称轴在y轴的右侧，即﹣ ＞0得ab＜0，故④不正确；由此即可得出答案.
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
