题目内容
【题目】如图,直线y=x+b与抛物线y=![]() x2+
x2+![]() x+c相交于点A(6,8)与点B,P是线段AB的中点,D是抛物线上的一个动点,直线DP交x轴于点C.
x+c相交于点A(6,8)与点B,P是线段AB的中点,D是抛物线上的一个动点,直线DP交x轴于点C.
(1)分别求出这两个函数的关系式,并写出点B,P的坐标.
(2)四边形ACBD能否成为平行四边形?若能,请求出线段OC的长度;若不能,请说明理由.
(3)当点D的坐标为(4,2)时,△APD是什么特殊三角形?请说明理由,并写出所有符合这一特殊性的点D的坐标.



【答案】(1)(-4,-2),(1,3);(2)OC=![]() -3或
-3或![]() +3;(3)符合△APD是直角三角的点D还有:(-12,26),(-3+
+3;(3)符合△APD是直角三角的点D还有:(-12,26),(-3+![]() ,7-
,7-![]() ),(-3-
),(-3-![]() ,7+
,7+![]() ).
).
【解析】
(1)利用待定系数法,把点A的坐标分别代入y=x+b和y=![]() x2+
x2+![]() x+c,
x+c,
得b=2,c=-4,求得函数关系式为:y=x+2,y=![]() x2+
x2+![]() x-4,从而求出点B,P的坐标分别为(-4,-2),(1,3),
x-4,从而求出点B,P的坐标分别为(-4,-2),(1,3),
(2)作PE⊥x轴于E,DF⊥x轴于F,则DF=2PE=6,当y=6时,![]() x2+
x2+![]() x-4=6,解得x=-1±
x-4=6,解得x=-1±![]() ,然后分情况讨论:当点C在直线AB的左侧时(如答图1),OF=
,然后分情况讨论:当点C在直线AB的左侧时(如答图1),OF=![]() -1,进而可得:CE=EF=OF-OE=(
-1,进而可得:CE=EF=OF-OE=(![]() -1)-1=
-1)-1=![]() -2.因此可得:OC=CE-OE=(
-2.因此可得:OC=CE-OE=(![]() -2)-1=
-2)-1=![]() -3;当点C在直线AB的左侧时(如答图2),OF=
-3;当点C在直线AB的左侧时(如答图2),OF=![]() +1,进而可得:CE=EF=OF+OE=(
+1,进而可得:CE=EF=OF+OE=(![]() +1)+1=
+1)+1=![]() +2,从而可得:OC=CE+OE=(
+2,从而可得:OC=CE+OE=(![]() +2)+1=
+2)+1=![]() +3.
+3.
(3)作PE⊥BC于E,作DF⊥BC于F,AG⊥BC于G,过点D作MN分别垂直AG,PE于M,N,可得:EN=DF=MG=2,DN=EF=OF-OE=3,DM=FG=6-4=2,AM=AG-MG=6进而可得:DP=![]() ,AD=2
,AD=2![]() ,根据AP=5
,根据AP=5![]() ,可得:DP2+AD2=AP2,根据勾股定理逆定理可得:∠ADP=90,即△APD是直角三角形,符合△APD是直角三角的点D还有:(-12,26),(-3+
,可得:DP2+AD2=AP2,根据勾股定理逆定理可得:∠ADP=90,即△APD是直角三角形,符合△APD是直角三角的点D还有:(-12,26),(-3+![]() ,7-
,7-![]() ),(-3-
),(-3-![]() ,7+
,7+![]() ).
).
(1)把点A的坐标分别代入y=x+b和y=![]() x2+
x2+![]() x+c,
x+c,
得b=2,c=-4,
∴y=x+2,y=![]() x2+
x2+![]() x-4,
x-4,
点B,P的坐标分别为(-4,-2),(1,3),
(2)作PE⊥x轴于E,DF⊥x轴于F,则DF=2PE=6,
当y=6时,![]() x2+
x2+![]() x-4=6,解得x=-1±
x-4=6,解得x=-1±![]() ,
,
当点C在直线AB的左侧时(如答图1),OF=![]() -1,
-1,
∴CE=EF=OF-OE=(![]() -1)-1=
-1)-1=![]() -2.
-2.
∴OC=CE-OE=(![]() -2)-1=
-2)-1=![]() -3.
-3.
当点C在直线AB的左侧时(如答图2),OF=![]() +1,
+1,
∴CE=EF=OF+OE=(![]() +1)+1=
+1)+1=![]() +2,
+2,
∴OC=CE+OE=(![]() +2)+1=
+2)+1=![]() +3.
+3.
综上所述,OC=![]() -3或
-3或![]() +3,
+3,
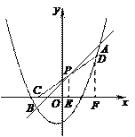

答图1 答图2 答图3
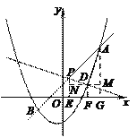
(3)当点D的坐标为(4,2)时,△APD是直角三角形,理由如下:
如答图3,作PE⊥BC于E,作DF⊥BC于F,AG⊥BC于G,
过点D作MN分别垂直AG,PE于M,N,
则EN=DF=MG=2,DN=EF=OF-OE=3,DM=FG=6-4=2,
AM=AG-MG=6.
∴DP=![]() ,AD=2
,AD=2![]() ,
,
∵AP=5![]() ,
,
∴DP2+AD2=AP2,
∴∠ADP=90,即△APD是直角三角形(用相似证明同样给分),
符合△APD是直角三角的点D还有:(-12,26),(-3+![]() ,7-
,7-![]() ),
),
(-3-![]() ,7+
,7+![]() ).
).

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】某小组在学校组织的研究性学习活动中了解所居住的小区500户居民的人均收入情况,从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图,根据以上提供的信息,解答下列问题:
分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合计 | 40 | 100% |
(1)补全频数分布表.
(2)补全频数分布直方图.

(3)请你估计该居民小区家庭人均收入属于中等收入(1000≤x<1600)的大约有多少户?