题目内容
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣2,0),B(0,![]() ),C(4,0),其对称轴与x轴交于点D,若P为y轴上的一个动点,连接PD,
),C(4,0),其对称轴与x轴交于点D,若P为y轴上的一个动点,连接PD,![]() PB+PD的最小值为________.
PB+PD的最小值为________.

【答案】![]()
【解析】
如图所示,连接AB,作DH⊥AB于H,交OB于P,由于OA=2,OB=![]() ,
,
因此![]() ,根据特殊三角函数值可得:
,根据特殊三角函数值可得:![]() ,根据特殊直角三角形的性质可得:PH=
,根据特殊直角三角形的性质可得:PH=![]() ,即
,即![]() ,则此时
,则此时![]() 最小,在Rt△ADH中,根据
最小,在Rt△ADH中,根据![]() ,AD=3,
,AD=3,![]() ,由此可得:
,由此可得:![]() ,解得:
,解得:![]() ,即
,即![]() 最小值为:
最小值为:![]() .
.
如图所示,连接AB,作DH⊥AB于H,交OB于P,此时![]() 最小,
最小,
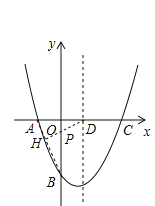
理由:因为OA=2,OB=![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以PH=![]() ,
,
所以![]() ,
,
所以此时![]() 最小,
最小,
在Rt△ADH中,因为![]() ,AD=3,
,AD=3,![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() 最小值为:
最小值为:![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目






