题目内容
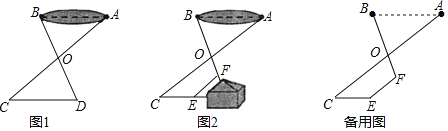
【题目】如图1,为测量池塘宽度AB,可在池塘外的空地上取任意一点O,连接AO,BO,并分别延长至点C,D,使OC=OA,OD=OB,连接CD
(1)求证:AB=CD;
(2)如图2,受地形条件的影响,于是采取以下措施:延长AO至点C,使OC=OA,过点C作AB的平行线CE,延长BO至点F,连接EF,测得∠CEF=140°,∠OFE=110°,CE=11m,EF=10m,请直接写出池塘宽度AB.
【答案】(1)见解析;(2)21m
【解析】
(1)利用SAS证明△ABO≌△CDO即可;
(2)延长OF、CE交于点G,求出EF=EG,进而得到CG的长度,然后证明△ABO≌△CGO,根据全等三角形的性质解答.
(1)在△ABO与△CDO中,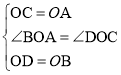 ,
,
∴△ABO≌△CDO(SAS),
∴AB=CD;
(2)如图所示:
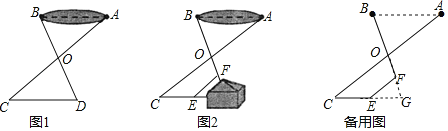
延长OF、CE交于点G,
∵∠CEF=140°,∠OFE=110°,
∴∠FEG=40°,∠EFG=70°,
∴∠G=180°﹣40°﹣70°=70°,
∴EF=EG,
∵CE=11m,EF=10m,
∴CG=CE+EG=CE+EF=11+10=21m,
∵CG∥AB,
∴∠A=∠C,
在△ABO与△CGO中,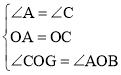 ,
,
∴△ABO≌△CGO(ASA)
∴AB=CG=21m.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目