Question

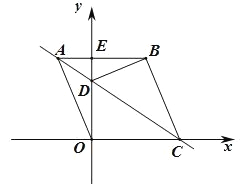
【题目】已知，如图，O为坐标原点，四边形OABC为矩形，B（5，2），点D是OA的中点，动点P在线段BC上以每秒2个单位长的速度由点C向B 运动．设动点P的运动时间为t秒

（1）当t为何值时，四边形PODB是平行四边形？

（2）在直线CB上是否存在一点Q，使得O、D、Q、P四点为顶点的四边形是菱形？若存在，求t的值，并求出Q点的坐标；若不存在，请说明理由．

（3）在线段PB上有一点M，且PM＝2.5，当P运动多少，四边形OAMP的周长最小值为多少，并画图标出点M的位置．

Answer 1

【答案】（1）t＝1.25；（2）①Q（4，2）；②Q（1.5，2），③Q（﹣1.5，2）；（3）、．

【解析】

（1）先求出OA，进而求出OD=2.5，再由运动知BP=5-2t，进而由平行四边形的性质建立方程5-2t=2.5即可得出结论；
（2）分三种情况讨论，利用菱形的性质和勾股定理即可得出结论；
（3）先判断出四边形OAMP周长最小，得出AM+DM最小，即可确定出点M的位置，再用三角形的中位线得出BM，进而求出PC，即可得出结论．

（1）∵四边形OABC为矩形，B（5，2），

∴BC＝OA＝5，AB＝OC＝2，

∵点D时OA的中点，

∴OD＝OA＝2.5，

由运动知，PC＝2t，

∴BP＝BC﹣PC＝5﹣2t，

∵四边形PODB是平行四边形，

∴PB＝OD＝2.5，

∴5﹣2t＝2.5，

∴t＝1.25；

（2）①当Q点在P的右边时，如图1，

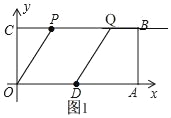
∵四边形ODQP为菱形，

∴OD＝OP＝PQ＝2.5，

∴在Rt△OPC中，由勾股定理得：PC＝1.5，

∴2t＝1.5；

∴t＝0.75，

∴Q（4，2）；

②当Q点在P的左边且在BC线段上时，如图2，

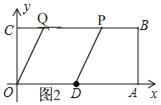
同①的方法得出t＝2，

∴Q（1.5，2），

③当Q点在P的左边且在BC的延长线上时，如图3，

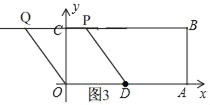
同①的方法得出，t＝0.5，

∴Q（﹣1.5，2）；

（3）t＝

如图4，

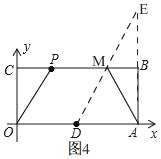
由（1）知，OD＝2.5，

∵PM＝2.5，

∴OD＝PM，

∵BC∥OA，

∴四边形OPMD时平行四边形，

∴OP＝DM，

∵四边形OAMP的周长为OA+AM+PM+OP＝5+AM+2.5+DM＝7.5+AM+DM，

∴当AM+DM最小时，四边形OAMP的周长最小，

∴作点A关于BC的对称点E，连接DE交PB于M，

∴AB＝EB，

∵BC∥OA，

∴BM＝AD＝，

∴PC＝BC﹣BM﹣PM＝5﹣﹣＝，DM+AM＝DE＝＝＝，

∴t＝÷2＝，周长的最小值为．