Question

【题目】（1）计算：2﹣1+（π﹣3.14）0+sin60°﹣|﹣|

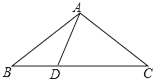
（2）如图，在△ABC中，AB=AC=10，sinC=，点D是BC上一点，且DC=AC．求BD的长．

Answer 1

【答案】（1） （2）6

【解析】

（1）分别根据0指数幂、负整数指数幂、特殊角的三角函数值即绝对值的性质计算出各数，再根据实数混合运算的法则进行计算即可；
（2）过点A作AE⊥BC于点E，根据等腰三角形的性质得出BE=CE，在Rt△ACE中根据AC=10，sin∠C=，得出AE=6，由勾股定理求出CE的值，再由BD=BC-BD=BC-AC即可得出结论．

（1）解：原式=+1+﹣

=；

（2）解：过点A作AE⊥BC于点E，

∵AB=AC，

∴BE=CE，

在Rt△ACE中，AC=10，sin∠C= ，

∴AE=6，

∴CE==8，

∴BD=2CE=16，

∴BD=BC﹣BD=BC﹣AC=6．