题目内容
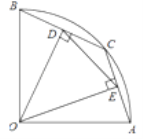
【题目】如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧 AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为点D,E;在点C的运动过程中,下列说法正确的是( )
A. 扇形AOB的面积为![]() B. 弧BC的长为
B. 弧BC的长为![]() C. ∠DOE=45° D. 线段DE的长是
C. ∠DOE=45° D. 线段DE的长是![]()
【答案】C
【解析】
根据扇形的公式可求出扇形的面积,判断A是否正确;根据弧长公式和动点C,可判断B;根据垂径定理可判断∠DOE=45°;连接AB,用勾股定理可求出AB的长,根据垂径定理可得D和E分别是线段BC和AC的中点,根据三角形中位线定理就可得到DE=![]() AB,即可得到DE的长.
AB,即可得到DE的长.
根据扇形的面积公式,由r=2,∠AOB=90°,可得![]() =π,故A不正确;
=π,故A不正确;
根据弧长公式,由C点是是弧 AB上的一个动点(不与点A、B重合),可知弧BC的长不确定,故B不正确;
根据垂径定理,连接OC,可知∠BOD=∠COD,∠COE=∠AOE,因此可得∠COD+∠COE=![]() ∠AOB=45°,故C正确;
∠AOB=45°,故C正确;
连接AB,连接AB,如图,

∵∠AOB=90°,OA=OB=5,
∴AB=![]() ,
,
∵OD⊥BC,OE⊥AC,
∴D和E分别是线段BC和AC的中点,
∴DE=![]() AB=
AB=![]() ,
,
故D不正确.
故选:C.

练习册系列答案
相关题目