��Ŀ����
����Ŀ����ͼ1�����ı���ABCD�У���DAB���Խ���ACƽ�֣���AC2��ABAD�����dzƸ��ı���Ϊ���ɷ��ı���������DAB��Ϊ���ɷֽ�����
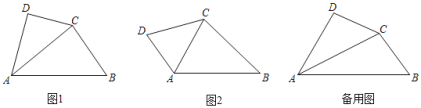
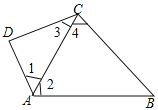
��1����ͼ2���ı���ABCDΪ���ɷ��ı���������DABΪ���ɷֽ�������֤����DAC�ס�CAB��
��2����ͼ2���ı���ABCDΪ���ɷ��ı���������DABΪ���ɷֽ����������DCB����DAB�����DAB�� ��
��3�������ı���ABCDΪ���ɷ��ı���������DABΪ���ɷֽ�������AC��4��BC��2����D��90������AD�ij�.
���𰸡���1������������2��120�㣻��3��![]()
��������
��1�����жϳ�![]() �����ɵó����ۣ�
�����ɵó����ۣ�
��2������֪������֤�á�ADC�ס�ACB���ó�D=��4��������֪�������������ڽǺͶ����ó���1+2��1=180���������1=60�������ɵó���DAB�Ķ�����
��3������֪�ó�AC2=ABAD����DAC=��CAB��֤����ADC�ס�ACB���ó���D=��ACB=90�����ɹ��ɶ������AB�����ɵó�AD�ij���
��1��֤�������ı���ABCDΪ���ɷ��ı���������DABΪ���ɷֽ�����
��AC2��ABAD��
��![]() ��
��
�ߡ�DABΪ���ɷֽ�����
���CAD����BAC��
���DAC�ס�CAB��
��2���⣺��ͼ��ʾ��
��ACƽ�֡�DAB��
���1����2��
��AC2��ABAD��
��AD��AC��AC��AB��
���ADC�ס�ACB��
���D����4��
�ߡ�DCB����DAB��
���DCB����3+��4��2��1��
�ߡ�1+��D+��3����1+��4+��3��180����
���1+2��1��180����
����1��60����
���DAB��120����
�ʴ�Ϊ��120��
��3���⣺���ı���ABCDΪ���ɷ��ı���������DABΪ���ɷֽ�����
��AC2��ABAD����DAC����CAB��
��AD��AC��AC��AB��
���ADC�ס�ACB��
���D����ACB��90����
��AB��![]() ��
��
��AD��![]() .
.
�ʴ�Ϊ![]() .
.