题目内容
【题目】已知△ABC中,AC=BC,∠C=120°,点D为AB边的中点,∠EDF=60°,DE、DF分别交AC、BC与E、F点。
(1)如图,若EF∥AB,求证DE=DF
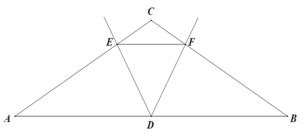
(2)如图,若EF与AB不平行,则问题(1)的结论是否成立?说明理由.

【答案】(1)证明见解析;(2)成立,理由见解析.
【解析】
(1)根据SAS证明△ADE≌△BDF,再根据全等三角形的性质可得DE=DF;
(2)过D作DM⊥AC交AC于M,再作DN⊥BC交BC于N.可证明DM=DN.再分一、当M与E重合时,N就一定与F重合.二、当M落在C、E之间时,N就一定落在B、F之间.三、当M落在A、E之间时,N就一定落在C、F之间.三种情况讨论即可求解.
解:(1)∵EF∥AB.
∴∠FEC=∠A=30°.
∠EFC=∠B=30°
∴EC=CF.
又∵AC=BC
∴AE=BF
D是AB中点.
∴DB=AD
∴△ADE≌△BDF.
∴DE=DF
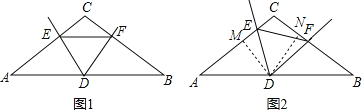
(2)如图2,过D作DM⊥AC交AC于M,再作DN⊥BC交BC于N.,
∵AC=BC,
∴∠A=∠B,
又∵∠ACB=120°,
∴∠A=∠B=(180°-∠ACB)÷2=30°,
∴∠ADM=∠BDN=60°,
∴∠MDN=180°-∠ADM-∠BDN=60°.
∵AC=BC、AD=BD,
∴∠ACD=∠BCD,
∴DM=DN.
由∠MDN=60°、∠EDF=60°,可知:
当M与E重合时,N就一定与F重合.此时:
DM=DE、DN=DF,结合证得的DM=DN,得:DE=DF,但EF∥AB,不合题意.
当M落在C、E之间时,N就一定落在B、F之间.此时:
∠EDM=∠EDF-∠MDF=60°-∠MDF,
∠FDN=∠MDN-∠MDF=60°-∠MDF,
∴∠EDM=∠FDN,
又∵∠DME=∠DNF=90°、DM=DN,
∴△DEM≌△DFN(ASA),
∴DE=DF.
当M落在A、E之间时,N就一定落在C、F之间.此时:
∠EDM=∠MDN-∠EDN=60°-∠EDN,
∠FDN=∠EDF-∠EDN=60°-∠EDN,
∴∠EDM=∠FDN,
又∵∠DME=∠DNF=90°、DM=DN,
∴△DEM≌△DFN(ASA),
∴DE=DF.
综上①②③所述,得:DE=DF.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?